
為了解七班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
| | 喜愛打籃球 | 不喜愛打籃球 | 合計 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合計 | | | 50 |
 .(12分)
.(12分) ,求
,求 的分布列與期望.
的分布列與期望. | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)
(1)列聯表見解析;(2)在犯錯誤的概率不超過0.005的前提下,認為喜愛打籃球與性別有關;(3) 的分布列見解析,期望為
的分布列見解析,期望為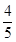 .
.
解析試題分析:(1)喜愛打籃球的學生的概率為 ,則喜愛打籃球人數為30,可不喜愛打籃球的人數為20,可由表中行可得男生人數,女生人數;(2)可求得
,則喜愛打籃球人數為30,可不喜愛打籃球的人數為20,可由表中行可得男生人數,女生人數;(2)可求得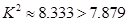 查表知不超過0.005的前提下,認為喜愛打籃球與性別有關;(3)喜愛打籃球的女生人數
查表知不超過0.005的前提下,認為喜愛打籃球與性別有關;(3)喜愛打籃球的女生人數 的可能取值為
的可能取值為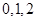 .分別求出概率,得出分布列,求出期望.
.分別求出概率,得出分布列,求出期望.
試題解析:解:(1) 列聯表補充如下: 3分 喜愛打籃球 不喜愛打籃球 合計 男生 20 5 25 女生 10 15 25 合計 30 20 50
(2)∵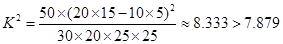
∴在犯錯誤的概率不超過0.005的前提下,認為喜愛打籃球與性別有關. 7分
(3)喜愛打籃球的女生人數 的可能取值為
的可能取值為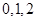 .
.
其概率分別為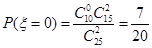 ,
, ,
,
故 的分布列為:
的分布列為:

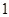
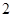
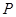
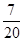
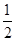
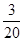
 的期望值為:
的期望值為: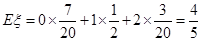


科目:高中數學 來源: 題型:解答題
甲、乙兩袋裝有大小相同的紅球和白球,甲袋裝有2個紅球,2個白球;乙袋裝有2個紅球,n個白球.現從甲,乙兩袋中各任取2個球.
(Ⅰ)若n=3,求取到的4個球全是紅球的概率;
(Ⅱ)若取到的4個球中至少有2個紅球的概率為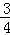 ,求n.
,求n.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某班學生關注NBA是否與性別有關,對本班48人進行了問卷調查得到如下的列聯表:
| | 關注NBA | 不關注NBA | 合 計 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 計 | | | 48 |
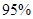 的把握認為關注NBA與性別有關?
的把握認為關注NBA與性別有關?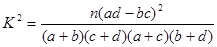 ,其中
,其中 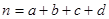
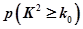 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某家電專賣店在五一期間設計一項有獎促銷活動,每購買一臺電視,即可通過電腦產生一組3個數的隨機數組,根據下表兌獎:
| 獎次 | 一等獎 | 二等獎 | 三等獎 |
| 隨機數組的特征 | 3個1或3個0 | 只有2個1或2個0 | 只有1個1或1個0 |
| 資金(單位:元) | 5m | 2m | m |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
小王經營一家面包店,每天從生產商處訂購一種品牌現烤面包出售.已知每賣出一個現烤面包可獲利10元,若當天賣不完,則未賣出的現烤面包因過期每個虧損5元.經統計,得到在某月(30天)中,小王每天售出的現烤面包個數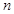 及天數如下表:
及天數如下表:
售出個數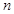 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天數 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
自駕游從A地到B地有甲乙兩條線路,甲線路是A-C-D-B,乙線路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵車路段.假設這三條路段堵車與否相互獨立.這三條路段的堵車概率及平均堵車時間如表所示.
| | CD段 | EF段 | GH段 |
| 堵車概率 | 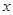 | 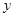 | 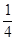 |
| 平均堵車時間 (單位:小時) |  | 2 | 1 |
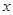 在
在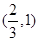 上變化,
上變化,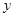 在
在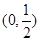 上變化.
上變化.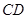 段平均堵車時間,調查了100名走甲線路的司機,得到下表數據.
段平均堵車時間,調查了100名走甲線路的司機,得到下表數據.| 堵車時間(單位:小時) | 頻數 |
| [0,1] | 8 |
| (1, 2] | 6 |
| (2, 3] | 38 |
| (3, 4] | 24 |
| (4, 5] | 24 |
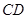 段平均堵車時間
段平均堵車時間 的值;
的值;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
深圳市某校中學生籃球隊假期集訓,集訓前共有6個籃球,其中3個是新球(即沒有用過的球),3個是舊球(即至少用過一次的球).每次訓練,都從中任意取出2個球,用完后放回.
(1)設第一次訓練時取到的新球個數為ξ,求ξ的分布列和數學期望;
(2)求第二次訓練時恰好取到一個新球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
乒乓球單打比賽在甲、乙兩名運動員間進行,比賽采用7局4勝制(即先勝4局者獲勝,比賽結束),假設兩人在每一局比賽中獲勝的可能性相同.
(1)求甲以4比1獲勝的概率;
(2)求乙獲勝且比賽局數多于5局的概率;
(3)求比賽局數的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
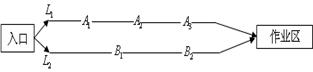
某煤礦發生透水事故時,作業區有若干人員被困.救援隊從入口進入之后有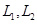 兩條巷道通往作業區(如下圖),
兩條巷道通往作業區(如下圖),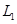 巷道有
巷道有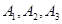 三個易堵塞點,各點被堵塞的概率都是
三個易堵塞點,各點被堵塞的概率都是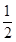 ;
;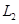 巷道有
巷道有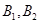 兩個易堵塞點,被堵塞的概率分別為
兩個易堵塞點,被堵塞的概率分別為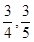 .
.
(1)求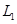 巷道中,三個易堵塞點最多有一個被堵塞的概率;
巷道中,三個易堵塞點最多有一個被堵塞的概率;
(2)若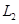 巷道中堵塞點個數為
巷道中堵塞點個數為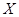 ,求
,求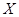 的分布列及數學期望
的分布列及數學期望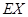 ,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com