
【題目】某企業(yè)接到生產(chǎn)3000臺某產(chǎn)品的![]() 三種部件的訂單,每臺產(chǎn)品需要這三種部件的數(shù)量分別為2,2,1(單位:件).已知每個工人每天可生產(chǎn)
三種部件的訂單,每臺產(chǎn)品需要這三種部件的數(shù)量分別為2,2,1(單位:件).已知每個工人每天可生產(chǎn)![]() 部件6件,或
部件6件,或![]() 部件3件,或
部件3件,或![]() 部件2件.該企業(yè)計劃安排200名工人分成三組分別生產(chǎn)這三種部件,生產(chǎn)
部件2件.該企業(yè)計劃安排200名工人分成三組分別生產(chǎn)這三種部件,生產(chǎn)![]() 部件的人數(shù)與生產(chǎn)
部件的人數(shù)與生產(chǎn)![]() 部件的人數(shù)成正比,比例系數(shù)為
部件的人數(shù)成正比,比例系數(shù)為![]() (
(![]() 為正整數(shù)).
為正整數(shù)).
(1)設(shè)生產(chǎn)![]() 部件的人數(shù)為
部件的人數(shù)為![]() ,分別寫出完成
,分別寫出完成![]() 三件部件生產(chǎn)需要的時間;
三件部件生產(chǎn)需要的時間;
(2)假設(shè)這三種部件的生產(chǎn)同時開工,試確定正整數(shù)![]() 的值,使完成訂單任務(wù)的時間最短,并給出時間最短時具體的人數(shù)分組方案.
的值,使完成訂單任務(wù)的時間最短,并給出時間最短時具體的人數(shù)分組方案.
【答案】(1)A:![]() ,B:
,B:![]() ,C:
,C:![]() ,其中
,其中![]() 均為1到200之間的正整數(shù);(2)當(dāng)
均為1到200之間的正整數(shù);(2)當(dāng)![]() 時,完成訂單任務(wù)的時間最短,此時,生產(chǎn)
時,完成訂單任務(wù)的時間最短,此時,生產(chǎn)![]() 三種部件的人數(shù)分別為44,88,68.
三種部件的人數(shù)分別為44,88,68.
【解析】
試題分析:(1)產(chǎn)品件數(shù)都是3000,關(guān)鍵是求出人數(shù)分配,由題意生產(chǎn)A部件人數(shù)為![]() ,則B有
,則B有![]() 人,C有
人,C有![]() 人,這樣由產(chǎn)品件數(shù)除以人數(shù)可得時間;(2)
人,這樣由產(chǎn)品件數(shù)除以人數(shù)可得時間;(2)![]() 的最大值就是完成任務(wù)所需時間,記為
的最大值就是完成任務(wù)所需時間,記為![]() ,注意到
,注意到![]() ,為了求
,為了求![]() 最小值,因此可分類
最小值,因此可分類![]() 和
和![]() ,
,![]() 為減函數(shù),
為減函數(shù),![]() 為增函數(shù),
為增函數(shù),![]() 時,
時,![]() ,在
,在![]() 時,
時,![]() 取得最小值,當(dāng)
取得最小值,當(dāng)![]() 時,
時,![]() ,此時
,此時![]()
![]() ,因此
,因此![]()
![]() ,由于
,由于![]() 是遞增,因此也量
是遞增,因此也量![]() 時,
時,![]() 取得最小值,比較兩個最小值的大小后發(fā)現(xiàn)
取得最小值,比較兩個最小值的大小后發(fā)現(xiàn)![]() 時更小,從而確定
時更小,從而確定![]() 時,時間最小.
時,時間最小.
試題解析:(1)設(shè)完成![]() 三種部件的生產(chǎn)任務(wù)需要的時間(單位:天)分別為
三種部件的生產(chǎn)任務(wù)需要的時間(單位:天)分別為![]() ,由題設(shè)有
,由題設(shè)有![]() ,
,
![]() ,
,
其中![]() 均為1到200之間的正整數(shù)
均為1到200之間的正整數(shù)
(2)完成訂單任務(wù)的時間為![]() .
.
易知,![]() 為減函數(shù),
為減函數(shù),![]() 為增函數(shù),注意到
為增函數(shù),注意到![]() ,
,
于是①當(dāng)![]() 時,
時,![]() ,此時,
,此時,![]() ,
,
由函數(shù)![]() 的單調(diào)性知,當(dāng)
的單調(diào)性知,當(dāng)![]() 時,
時,![]() 取得最小值,解得
取得最小值,解得![]() ,
,
由于![]() ,而
,而![]() ,∵
,∵![]() ,
,
∴當(dāng)![]() 時完成訂單任務(wù)的時間最短,且最短時間為
時完成訂單任務(wù)的時間最短,且最短時間為![]()
②當(dāng)![]() 時,
時,![]() ,由于
,由于![]() 為正整數(shù),∴
為正整數(shù),∴![]() ,
,
此時,![]() .
.
記![]() ,易知,
,易知,![]() 是增函數(shù),
是增函數(shù),
則![]() ,
,
由函數(shù)![]() 的單調(diào)性知,當(dāng)
的單調(diào)性知,當(dāng)![]() 時,
時,![]() 取得最小值,解得
取得最小值,解得![]() ,
,
由于![]() ,而
,而![]() ,
,
此時,完成訂單任務(wù)的最短時間大于![]() .
.
綜上所述,當(dāng)![]() 時,完成訂單任務(wù)的時間最短,此時,生產(chǎn)
時,完成訂單任務(wù)的時間最短,此時,生產(chǎn)![]() 三種部件的人數(shù)分別為44,88,68.
三種部件的人數(shù)分別為44,88,68.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列框圖中,可作為流程圖的是( )
A.整數(shù)指數(shù)冪→有理指數(shù)冪→無理指數(shù)冪
B.隨機事件→頻率→概率
C.入庫→找書→閱覽→借書→出庫→還書
D.推理→圖像與性質(zhì)→定義
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列表述:①綜合法是由因?qū)Чǎ虎诰C合法是順推證法;③分析法是執(zhí)果索因法;④分析法是間接證法;⑤反證法是逆推證法;其中正確的是( )
A.①②③B.③④⑤C.①③④D.②③⑤
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() ,
,
①若f(a)=14,求a的值
②在平面直角坐標(biāo)系中,作出函數(shù)y=f(x)的草圖.(需標(biāo)注函數(shù)圖象與坐標(biāo)軸交點處所表示的實數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間將10名技工平均分為甲、乙兩組加工某種零件,在單位時間內(nèi)每名技工加工零件若干,其中合格零件的個數(shù)如下表:
1號 | 2號 | 3號 | 4號 | 5號 | |
甲組 | 4 | 5 | 7 | 9 | 10 |
乙組 | 5 | 6 | 7 | 8 | 9 |
(1)分別求出甲、乙兩組技工在單位時間內(nèi)完成合格零件的平均數(shù)及方差,并由此分析兩組技工的技術(shù)水平;
(2)質(zhì)檢部門從該車間甲、乙兩組中各隨機抽取一名技工,對其加工的零件進(jìn)行檢測,若兩人完成合格零件個數(shù)之和超過12件,則稱該車間“質(zhì)量合格”,求該車間“質(zhì)量合格”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,其焦點為
,其焦點為![]() .
.
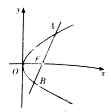
(1)若點![]() ,求以
,求以![]() 為中點的拋物線的弦所在的直線方程;
為中點的拋物線的弦所在的直線方程;
(2)若互相垂直的直線![]() 都經(jīng)過拋物線
都經(jīng)過拋物線![]() 的焦點
的焦點![]() ,且與拋物線相交于
,且與拋物線相交于![]() 兩點和
兩點和![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的最小值為
的最小值為![]() ,且
,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上不單調(diào),求實數(shù)
上不單調(diào),求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)在區(qū)間![]() 上,
上,![]() 的圖象恒在
的圖象恒在![]() 的圖象上方,試確定實數(shù)
的圖象上方,試確定實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com