
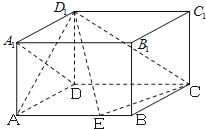
【題目】已知在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
(Ⅰ)求證:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在點E使得AD1與平面D1EC成的角為![]() ?若存在,求出AE的長,若不存在,說明理由.
?若存在,求出AE的長,若不存在,說明理由.
【答案】(Ⅰ)證明見解析;(2)![]() .
.
【解析】試題分析:
(Ⅰ)要證![]() ,由正方形有
,由正方形有![]() ,因此要證
,因此要證![]() 平面
平面![]() ,而要證此線面垂直,只要證
,而要證此線面垂直,只要證![]() ,這由長方體的性質可得;(Ⅱ)假設存在,以D為原點,建立空間直角坐標系,寫出各點坐標,并設
,這由長方體的性質可得;(Ⅱ)假設存在,以D為原點,建立空間直角坐標系,寫出各點坐標,并設![]() ,用向量法求出AD1與平面D1EC成的角,從而求出
,用向量法求出AD1與平面D1EC成的角,從而求出![]() ,若能求出
,若能求出![]() ,說明存在,若不能求出
,說明存在,若不能求出![]() ,說明不存在.
,說明不存在.
試題解析:
(Ⅰ)證明:∵AE⊥平面AA1DD1,A1D平面AA1DD1,
∴AE⊥A1D,
∵在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,
∴A1D⊥AD1,
∵AE∩AD1=A,∴A1D⊥平面AED1,
∵D1E平面AED1,∴A1D⊥D1E.
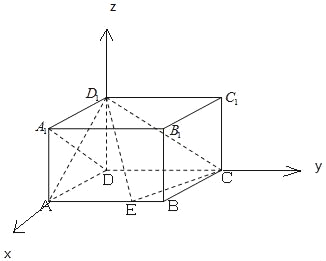
(Ⅱ)解:以D為原點,DA為x軸,DC為y軸,DD1為z軸,建立空間直角坐標系,
設棱AB上存在點E(1,t,0),(0≤t≤2),使得AD1與平面D1EC成的角為![]() ,
,
A(1,0,0),D1(0,0,1),C(0,2,0),
![]() =(﹣1,0,1),
=(﹣1,0,1),![]() =(0,﹣2,1),
=(0,﹣2,1),![]() =(1,t﹣2,0),
=(1,t﹣2,0),
設平面D1EC的法向量為![]() =(x,y,z),
=(x,y,z),
則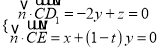 ,取y=1,得
,取y=1,得![]() =(t﹣1,1,2),
=(t﹣1,1,2),
∴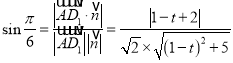 ,
,
整理,得t2﹣10t+12=0,
解得![]() 或
或![]() (舍),
(舍),
∴在棱AB上存在點E使得AD1與平面D1EC成的角為![]() ,AE=
,AE=![]() .
.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的參數方程為
的參數方程為 ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)求直線![]() 與曲線
與曲線![]() 的交點的直角坐標.
的交點的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①![]() 意味著每增加一個單位,
意味著每增加一個單位,![]() 平均增加8個單位
平均增加8個單位
②投擲一顆骰子實驗,有擲出的點數為奇數和擲出的點數為偶數兩個基本事件
③互斥事件不一定是對立事件,但對立事件一定是互斥事件
④在適宜的條件下種下一顆種子,觀察它是否發芽,這個實驗為古典概型
其中正確的命題有__________________.
查看答案和解析>>
科目:高中數學 來源: 題型:
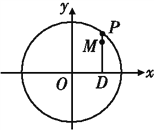
【題目】如圖,設P是圓![]() 上的動點,點D是P在x軸上的投影,M為線段PD上一點,且
上的動點,點D是P在x軸上的投影,M為線段PD上一點,且![]() ,
,
(1)當P在圓上運動時,求點M的軌跡C的方程;
(2)求過點(3,0)且斜率為![]() 的直線被軌跡C所截線段的長度.
的直線被軌跡C所截線段的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極點為直角坐標系的原點,極軸為x軸正半軸且單位長度相同的極坐標系中曲線C1:ρ=1, 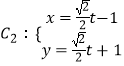 (t為參數).
(t為參數).
(Ⅰ)求曲線C1上的點到曲線C2距離的最小值;
(Ⅱ)若把C1上各點的橫坐標都擴大為原來的2倍,縱坐標擴大為原來的 ![]() 倍,得到曲線
倍,得到曲線 ![]() .設P(﹣1,1),曲線C2與
.設P(﹣1,1),曲線C2與 ![]() 交于A,B兩點,求|PA|+|PB|.
交于A,B兩點,求|PA|+|PB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 從
從![]() ,
, ![]() ,
, ![]() ,
, ![]() 四個數中任取的一個數,
四個數中任取的一個數, ![]() 是從
是從![]() ,
, ![]() ,
, ![]() 三個數中任取的一個數,求上述方程有實根的概率;
三個數中任取的一個數,求上述方程有實根的概率;
(2)若![]() 是從區間
是從區間![]() 上任取的一個數,
上任取的一個數, ![]() 是從區間
是從區間![]() 上任取的一個數,求上述方程有實根的概率.
上任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com