
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若不等式![]() 在
在![]() 時恒成立,求實數
時恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,證明:
時,證明:![]()
![]() .
.
【答案】(1)見解析;(2)![]() ;(3)見解析
;(3)見解析
【解析】分析:(1)求出![]() 的導函數
的導函數![]() ,由
,由![]() 得增區(qū)間,由
得增區(qū)間,由![]() 得減區(qū)間,注意在解不等式時要按
得減區(qū)間,注意在解不等式時要按![]() 的值分類討論;
的值分類討論;
(2)由(1)的結論知當![]() 時,
時,![]() ,題中不等式成立,而當
,題中不等式成立,而當![]() 時,題中不等式不恒成立;
時,題中不等式不恒成立;
(3)![]() 時,由(2)知
時,由(2)知![]() 上有
上有![]() ,從而
,從而![]() ,令
,令![]() ,然后所有不等式相加可證.
,然后所有不等式相加可證.
詳解: (1)∵y=f(x)-g(x)=ln(ax+1)-![]() ,
,
y′=![]() -
-![]() =
=![]() ,
,
當a≥1時,y′≥0,所以函數y=f(x)-g(x)是[0,+∞)上的增函數;
當0<a<1時,由y′>0得x>2![]() ,所以函數y=f(x)-g(x)在
,所以函數y=f(x)-g(x)在 上是單調遞增函數,函數y=f(x)-g(x)在
上是單調遞增函數,函數y=f(x)-g(x)在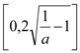 上是單調遞減函數;
上是單調遞減函數;
(2)當a≥1時,函數y=f(x)-g(x)是[0,+∞)上的增函數.
所以f(x)-g(x)≥f(0)-g(0)=1,
即不等式f(x)≥g(x)+1在x∈[0,+∞)時恒成立,
當0<a<1時,函數y=f(x)-g(x)是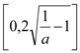 上的減函數,存在
上的減函數,存在 ,使得f(x0)-g(x0)<f(0)-g(0)=1,即不等式f(x0)≥g(x0)+1不成立,
,使得f(x0)-g(x0)<f(0)-g(0)=1,即不等式f(x0)≥g(x0)+1不成立,
綜上,實數a的取值范圍是[1,+∞).
(3)當a=1時,由(2)得不等式f(x)>g(x)+1在x∈(0,+∞)時恒成立,
即ln(x+1)>![]() ,所以
,所以![]() ,
,
即![]() <
<![]() [ln(k+1)-lnk].
[ln(k+1)-lnk].
所以![]() <
<![]() (ln2-ln1),
(ln2-ln1),
![]() <
<![]() (ln3-ln2),
(ln3-ln2),
![]() <
<![]() (ln4-ln3),…,
(ln4-ln3),…,
![]() <
<![]() [ln(n+1)-lnn].
[ln(n+1)-lnn].
將上面各式相加得到,![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() [(ln2-ln1)+(ln3-ln2)+(ln4-ln3)+…+(ln(n+1)-lnn)]=
[(ln2-ln1)+(ln3-ln2)+(ln4-ln3)+…+(ln(n+1)-lnn)]=![]() ln(n+1)=
ln(n+1)=![]() f(n).
f(n).
∴原不等式成立.


科目:高中數學 來源: 題型:
【題目】設函數f(x)的導函數為f′(x),若f(x)=![]() ex﹣f(0)x+
ex﹣f(0)x+![]() x2(e是自然對數的底數).
x2(e是自然對數的底數).
(1)求f(0)和f′(1)的值;
(2)若g(x)=![]() x2+a與函數f(x)的圖象在區(qū)間[﹣1,2]上恰有2兩個不同的交點,求實數a的取值范圍.
x2+a與函數f(x)的圖象在區(qū)間[﹣1,2]上恰有2兩個不同的交點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校有初級教師21人,中級教師14人,高級教師7人,現采用分層抽樣的方法從這些教師中抽取6人對績效工資情況進行調查.
(1)求應從初級教師,中級教師,高級教師中分別抽取的人數;
(2)若從抽取的6名教師中隨機抽取2名做進一步數據分析,求抽取的2名均為初級教師的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}中,a1=1,an+1=an+n,利用如圖所示的程序框圖計算該數列的第10項,則判斷框中應填的語句是( ) 
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】產能利用率是指實際產出與生產能力的比率,工r產能利用率是衡量工業(yè)生產經營狀況的重要指標.下圖為國家統計局發(fā)布的2015年至2018年第2季度我國工業(yè)產能利用率的折線圖.
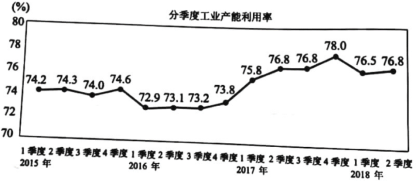
在統計學中,同比是指本期統計數據與上一年同期統計數據相比較,例如2016年第二季度與2015年第二季度相比較;環(huán)比是指本期統計數據與上期統計數據相比較,例如2015年第二季度與2015年第一季度相比較.
據上述信息,下列結論中正確的是( ).
A. 2015年第三季度環(huán)比有所提高B. 2016年第一季度同比有所提高
C. 2017年第三季度同比有所提高D. 2018年第一季度環(huán)比有所提高
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() :
:![]() ,點
,點![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() (不在y軸上).
(不在y軸上).

(1)若直線![]() 的斜率為3,求
的斜率為3,求![]() 的長度;
的長度;
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,求證:
,求證:![]() 為定值,并求出該定值;
為定值,并求出該定值;
(3)設![]() 的中點為
的中點為![]() ,是否存在直線
,是否存在直線![]() ,使得
,使得![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】旅行社為去廣西桂林的某旅游團包飛機去旅游,其中旅行社的包機費為10000元,旅游團中的每人的飛機票按以下方式與旅行社結算:若旅游團的人數在20或20以下,飛機票每人收費800元;若旅游團的人數多于20,則實行優(yōu)惠方案,每多1人,機票費每張減少10元,但旅游團的人數最多為75,則該旅行社可獲得利潤的最大值為( )
A. 12000元B. 15000元C. 12500元D. 20000元
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com