Question

已知函數y＝f(x)對于任意(k∈Z)，都有式子f(a－tanθ)＝cotθ－1成立(其中a為常數)．

(Ⅰ)求函數y＝f(x)的解析式；

(Ⅱ)利用函數y＝f(x)構造一個數列，方法如下：

對于給定的定義域中的x₁，令x₂＝f(x₁)，x₃＝f(x₂)，…，x_n＝f(x_n－1)，…在上述構造過程中，如果x_i(i＝1，2，3，…)在定義域中，那么構造數列的過程繼續下去；如果x_i不在定義域中，那么構造數列的過程就停止．

(ⅰ)如果可以用上述方法構造出一個常數列，求a的取值范圍；

(ⅱ)是否存在一個實數a，使得取定義域中的任一值作為x₁，都可用上述方法構造出一個無窮數列{x_n}？若存在，求出a的值；若不存在，請說明理由；

(ⅲ)當a＝1時，若x₁＝－1，求數列{x_n}的通項公式．

Answer 1

答案：
解析：

　　(Ⅰ)令x＝a－tanθ()，則tanθ＝a－x，而，

　　故＝，

　　∴＝()．……………3分

　　(Ⅱ)(ⅰ)根據題意，只需當時，方程有解，…………4分

　　亦即方程有不等于的解．

　　將代入方程左邊，左邊為1，與右邊不相等．故方程不可能有解．…………5分

　　由△＝，得或，

　　即實數a的取值范圍是．………7分

　　(ⅱ)假設存在一個實數a，使得取定義域中的任一值作為x₁，都可以用上述方法構造出一個無窮數列{x_n}，那么根據題意可知，＝在R中無解，……8分

　　亦即當x≠a時，方程(1＋a)x＝a²＋a－1無實數解．

　　由于不是方程的解，

　　所以對于任意x∈R，方程無實數解，

　　因此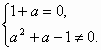解得．

　　∴即為所求的值．…………………11分

　　(ⅲ)當時，，所以，．

　　兩邊取倒數，得，即．

　　所以數列{}是首項為，公差的等差數列．

　　故，所以，，

　　即數列的通項公式為．……………14分