Question

函數的反函數是（ ）
A．y=e^2x-1-1（x＞0）
B．y=e^2x-1+1（x＞0）
C．y=e^2x-1-1（x∈R）
D．y=e^2x-1+1（x∈R）

Answer 1

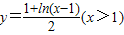
【答案】分析：從條件中中反解出x，再將x，y互換即得．解答本題首先熟悉反函數的概念，然后根據反函數求解三步驟：1、換：x、y換位，2、解：解出y，3、標：標出定義域，據此即可求得反函數．
解答：解：由原函數解得
x=e ^2y-1+1，
∴f^-1（x）=e ^2x-1+1，
又x＞1，∴x-1＞0；
∴ln（x-1）∈R∴在反函數中x∈R，
故選D．
點評：求反函數，一般應分以下步驟：（1）由已知解析式y=f（x）反求出x=Ф（y）；（2）交換x=Ф（y）中x、y的位置；（3）求出反函數的定義域（一般可通過求原函數的值域的方法求反函數的定義域）．