
【題目】求函數y= ![]() 的定義域、值域和單調區間.
的定義域、值域和單調區間.
【答案】解:根據題意,函數的定義域顯然為(﹣∞,+∞).
令u=f(x)=3+2x﹣x2=4﹣(x﹣1)2≤4.
∴y=3u是u的增函數,
當x=1時,ymax=f(1)=81,而y= ![]() >0.
>0.
∴0<3u≤34 , 即值域為(0,81].
當x≤1時,u=f(x)為增函數,y=3u是u的增函數,
由x越大推出u越大,u越大推出y越大
即x越大y越大
∴即原函數單調增區間為(﹣∞,1];
其證明如下:
任取x1 , x2∈(﹣∞,1]且令x1<x2
則 ![]() =
= ![]() ÷
÷ ![]() =
= ![]() =
= ![]() =
=![]()
∵x1<x2 , x1 , x2∈(﹣∞,1]
∴x1﹣x2<0,2﹣x1﹣x2>0
∴(x1﹣x2)(2﹣x1﹣x2)<0
∴ ![]() <1
<1
∴f(x1)<f(x2)
∴原函數單調增區間為(﹣∞,1]
當x>1時,u=f(x)為減函數,y=3u是u的增函數,
由x越大推出u越小,u越小推出y越小,
即x越大y越小
∴即原函數單調減區間為[1,+∞).
證明同上.
【解析】根據題意,定義域的求解易知為(﹣∞,+∞),值域的求解通過換元法將3+2x﹣x2換成u,通過二次函數的知識求得u的范圍為(﹣∞,4],再根據指數函數y=3u的單調性即可求解
利用復合函數的單調性的特點(根據同增異減口訣,先判斷內層函數的單調性,再判斷外層函數單調性,在同一定義域上,若兩函數單調性相同,則此復合函數在此定義域上為增函數,反之則為減函數)判斷出函數的單調區間,在根據定義:(就是定義域內的任意取x1 , x2 , 且x1<x2 , 比較f(x1),f(x2)的大小,或f(x1)<f(x2)則是增函數;反之則為減函數)證明即可
【考點精析】本題主要考查了指數函數的單調性與特殊點的相關知識點,需要掌握0<a<1時:在定義域上是單調減函數;a>1時:在定義域上是單調增函數才能正確解答此題.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】軸截面是邊長為4 ![]() 的等邊三角形的圓錐的直觀圖如圖所示,過底面圓周上任一點作一平面α,且α與底面所成的二面角為
的等邊三角形的圓錐的直觀圖如圖所示,過底面圓周上任一點作一平面α,且α與底面所成的二面角為 ![]() ,已知α與圓錐側面交線的曲線為橢圓,則此橢圓的離心率為( )
,已知α與圓錐側面交線的曲線為橢圓,則此橢圓的離心率為( ) 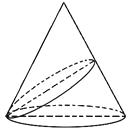
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家具廠生產一種課桌,每張課桌的成本為50元,出廠單價定為80元,該廠為鼓勵銷售商多訂購,決定一次訂購量超過100張時,每超過一張,這批訂購的全部課桌出廠單價降低0.02元.根據市場調查,銷售商一次訂購量不會超過1000張.
(1)設一次訂購量為x張,課桌的實際出廠單價為P元,求P關于x的函數關系式P(x);
(2)當一次訂購量x為多少時,該家具廠這次銷售課桌所獲得的利潤f(x)最大?其最大利潤是多少元?(家具廠售出一張課桌的利潤=實際出廠單價﹣成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別是a,b,c,已知2cosA(bcosC+ccosB)=a.
(1)求角A;
(2)若a= ![]() ,b+c=5,求△ABC的面積.
,b+c=5,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x∈[1,12],x2﹣a≥0.命題q:x0∈R,使得x02+(a﹣1)x0+1<0.若p或q為真,p且q為假,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
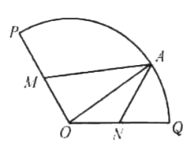
【題目】某校有一塊圓心![]() ,半徑為200米,圓心角為
,半徑為200米,圓心角為![]() 的扇形綠地
的扇形綠地![]() ,半徑
,半徑![]() 的中點分別為
的中點分別為![]() ,
,![]() 為弧
為弧![]() 上的一點,設
上的一點,設![]() ,如圖所示,擬準備兩套方案對該綠地再利用.
,如圖所示,擬準備兩套方案對該綠地再利用.
(1)方案一:將四邊形綠地![]() 建成觀賞魚池,其面積記為
建成觀賞魚池,其面積記為![]() ,試將
,試將![]() 表示為關于
表示為關于![]() 的函數關系式,并求
的函數關系式,并求![]() 為何值時,
為何值時,![]() 取得最大?
取得最大?
(2)方案二:將弧![]() 和線段
和線段![]() 圍成區域建成活動場地,其面積記為
圍成區域建成活動場地,其面積記為![]() ,試將
,試將![]() 表示為關于
表示為關于![]() 的函數關系式;并求
的函數關系式;并求![]() 為何值時,
為何值時,![]() 取得最大?
取得最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高二(1)班學生為了籌措經費給班上購買課外讀物,班委會成立了一個社會實踐小組,決定利用暑假八月份(30天計算)輪流換班去銷售一種時令水果.在這30天內每斤水果的收入![]() (元)與時間
(元)與時間![]() (天)的部分數據如下表所示,已知日銷售
(天)的部分數據如下表所示,已知日銷售![]() (斤)與時間
(斤)與時間![]() (天)滿足一次函數關系.
(天)滿足一次函數關系.
(1)根據提供的圖象和表格,下廚每斤水果的收入![]() (元)與時間
(元)與時間![]() (天)所滿足的函數關系式及日銷售量
(天)所滿足的函數關系式及日銷售量![]() (斤)與時間
(斤)與時間![]() (天)的一次函數關系;
(天)的一次函數關系;
(2)用![]() (元)表示銷售水果的日收入,寫出
(元)表示銷售水果的日收入,寫出![]() 與
與![]() 的函數關系式,并求這30天中第幾天日收入最大,最大值為多少元?
的函數關系式,并求這30天中第幾天日收入最大,最大值為多少元?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com