
已知函數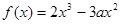 ,
, ,又函數
,又函數 在
在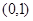 單調遞減,而在
單調遞減,而在 單調遞增.
單調遞增.
(1)求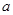 的值;
的值;
(2)求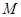 的最小值,使對
的最小值,使對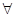
 ,有
,有 成立;
成立;
(3)是否存在正實數 ,使得
,使得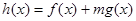 在
在 上既有最大值又有最小值?若存在,求出m的取值范圍;若不存在,請說明理由.
上既有最大值又有最小值?若存在,求出m的取值范圍;若不存在,請說明理由.
(1) ,(2)滿足條件的
,(2)滿足條件的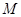 的最小值為52. (3)
的最小值為52. (3)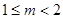
【解析】(1)由題意知x=1是函數f(x)的極小值點,所以可根據 求出a的值.
求出a的值.
(2)分別求出f(x)和g(x)在區間[-2,2]上的最值,再求出f(x)-g(x)的取值范圍,進而求出|f(x)-g(x)|的最大值即可,那么M的最小值就等于|f(x)-g(x)|的最大值.
(1)由題意知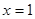 是函數
是函數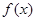 的一個極值點,即
的一個極值點,即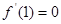 ,∴
,∴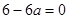 ,即
,即 ,
,
此時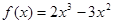 ,
, 滿足條件,∴
滿足條件,∴ .………4分
.………4分
(2)由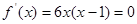 得,
得,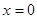 或
或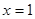 ,列表可得,
,列表可得,
 ,
,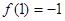 ,
, ,
, ,∴當
,∴當 時,
時,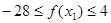 ;…………………6分
;…………………6分
又 ,∴當
,∴當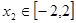 時,
時,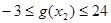 ;………8分
;………8分
因此,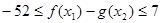 ,∴
,∴ ;∴滿足條件的
;∴滿足條件的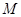 的最小值為52.……
10分
的最小值為52.……
10分
(3)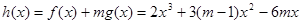
則 得
得 ;………12分
;………12分
要使得存在正實數 ,使得
,使得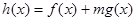 在
在 上既有最大值又有最小值,則必須
上既有最大值又有最小值,則必須 ,即
,即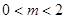 ,且滿足
,且滿足
 ,……………14分
,……………14分
得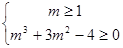 ,即
,即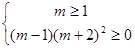 ∴
∴ ∴
∴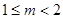 即為所求
即為所求


 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com