【題目】一對夫婦為了給他們的獨生孩子支付將來上大學的費用，從孩子一周歲生日開始，每年到銀行儲蓄
元一年定期，若年利率為
保持不變，且每年到期時存款（含利息）自動轉為新的一年定期，當孩子18歲生日時不再存入，將所有存款（含利息）全部取回，則取回的錢的總數為
A.
B.
C.
D.
輕松課堂單元期中期末專題沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】已知直線l： 
橢圓C： 
，
分別為橢圓的左右焦點.
（1）當直線l過右焦點
時，求C的標準方程；
（2）設直線l與橢圓C交于A，B兩點，O為坐標原點，若∠AOB是鈍角，求實數a的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的離心率為
，焦距為
.
（1）求的方程；
（2）若斜率為
的直線
與橢圓交于
，
兩點（點，均在第一象限），
為坐標原點.
①證明：直線
的斜率依次成等比數列.
②若
與關于
軸對稱，證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三梭柱ABC－A1B1C1中，AC＝BC，E，F分別為AB，A1B1的中點．
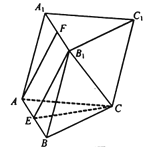
（1）求證：AF∥平面B1CE；
（2）若A1B1⊥
,求證：平面B1CE⊥平面ABC.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某企業生產的某種產品中抽取100件，測量這些產品的一項質量指標值．經數據處理后得到該樣本的頻率分布直方圖，其中質量指標值不大于1.50的莖葉圖如圖所示，以這100件產品的質量指標值在各區間內的頻率代替相應區間的概率．
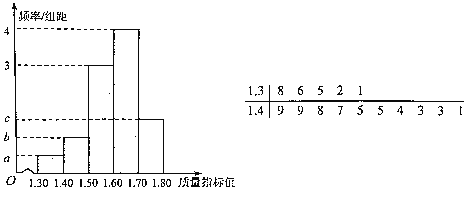
（1）求圖中
，
，
的值；
（2）估計這種產品質量指標值的平均數及方差（說明：①同一組中的數據用該組區間的中點值作代表；②方差的計算只需列式正確）；
（3）根據以上抽樣調查數據，能否認為該企業生產的這種產品符合“質量指標值不低于1.50的產品至少要占全部產品的
”的規定？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在10件產品中，有3件一等品，4件二等品，3件三等品。從這10件產品中任取3件，求：
（I） 取出的3件產品中一等品件數X的分布列和數學期望；
（II） 取出的3件產品中一等品件數多于二等品件數的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某部影片的盈利額（即影片的票房收入與固定成本之差）記為
,觀影人數記為
,其函數圖象如圖（1）所示.由于目前該片盈利未達到預期,相關人員提出了兩種調整方案,圖（2）、圖（3）中的實線分別為調整后與的函數圖象.
給出下列四種說法:
①圖（2）對應的方案是:提高票價,并提高成本;
②圖（2）對應的方案是:保持票價不變,并降低成本;
③圖（3）對應的方案是:提高票價,并保持成本不變;
④圖（3）對應的方案是:提高票價,并降低成本.
其中,正確的說法是____________.（填寫所有正確說法的編號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】改編自中國神話故事的動畫電影《哪吒之魔童降世》自7月26日首映，在不到一個月的時間，票房收入就超過了38億元，創造了中國動畫電影的神話.小明和同學相約去電影院觀看《哪吒之魔童降世》，影院的三個放映廳分別在7：30，8：00，8：30開始放映，小明和同學大約在7：40至8：30之間到達影院，且他們到達影院的時間是隨機的，那么他們到達后等待的時間不超過10分鐘的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
