Question

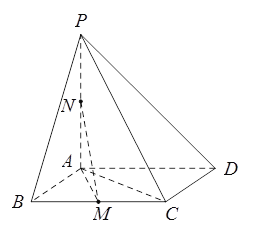
【題目】如圖，在四棱錐中，底面是平行四邊形， 平面，點， 分別為， 的中點，且， .

（1）證明： 平面；

（2）設(shè)直線與平面所成角為，當在內(nèi)變化時，求二面角的取值范圍.

Answer 1

【答案】(1) 見解析;(2) .

【解析】試題分析：（Ⅰ）根據(jù)直線與平面平行的判定定理，需在平面內(nèi)找一條與平行的直線.結(jié)合題設(shè)可取取中點，連接， 易得四邊形為平行四邊形，從而得，問題得證.

（Ⅱ）思路一、首先作出二面角的平面角，即過棱BC上一點分別在兩個平面內(nèi)作棱BC的垂線.因為，點分別為的中點，則.連接，因為平面，所以AM是PM在面ABC內(nèi)的射影，所以，所以即為二面角的平面角.再作出直線與平面所成的角，即作出AC在平面PBC內(nèi)的射影.由， 且得平面，從而平面平面.過點在平面內(nèi)作于，根據(jù)面面垂直的性質(zhì)知平面．連接，于是就是直線與平面所成的角．在及中，找出與的關(guān)系，即可根據(jù)的范圍求出的范圍. 思路二、以所在的直線分別為軸、軸、軸，建立空間直角坐標系，利用空間向量亦可求解.

試題解析：（Ⅰ）證明：取中點，連接，

因為點分別為的中點，所以

四邊形為平行四邊形，則又平面， 平面

所以平面.

（Ⅱ）解法1：連接，因為，點分別為的中點，則

又平面，則所以即為二面角的平面角

又，所以平面，則平面平面

過點在平面內(nèi)作于，則平面．

連接，于是就是直線與平面所成的角，即= ．

在中， ；

在中， ， ．

，

， ．

又， ．

即二面角取值范圍為．

解法2：連接，因為，點分別為的中點，則

又平面，則所以即為二面角的平面角，設(shè)為

以所在的直線分別為軸、軸、軸，建立如圖所示的空間直角坐標系，則，

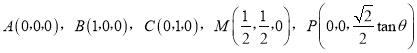于是， ， ， ．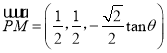

設(shè)平面的一個法向量為，

則由．

得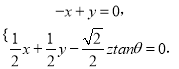

可取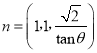，又，

于是，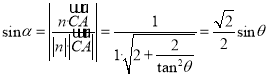

，

， ．

又， ．

即二面角取值范圍為．