
已知 ,函數
,函數 .
.
(I)證明:函數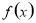 在
在 上單調遞增;
上單調遞增;
(Ⅱ)求函數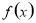 的零點.
的零點.
(I)詳見解析;(Ⅱ)詳見解析;
【解析】
試題分析:(I)先在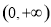 上任取兩變量
上任取兩變量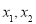 ,設
,設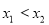 ,再對
,再對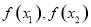 作差變形化簡,判斷
作差變形化簡,判斷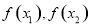 大小確定單調性.
大小確定單調性.
(Ⅱ)要求函數f(x)的零點,即求方程f(x)=0的根,對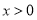 和
和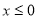 分情況求解,其中當
分情況求解,其中當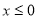 時,令
時,令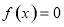 , 即
, 即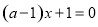 ,對此方程中參數a對根的情況進行討論求解.
,對此方程中參數a對根的情況進行討論求解.
試題解析: (1)證明:在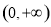 上任取兩個實數
上任取兩個實數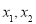 ,且
,且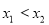 ,
,
則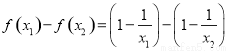

 . 2分
. 2分
∵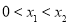 , ∴
, ∴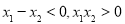 .
.
∴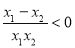 , 即
, 即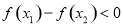 . ∴
. ∴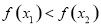 .
.
∴函數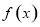 在
在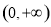 上單調遞增. 4分[K]
上單調遞增. 4分[K]
(2) (ⅰ)當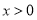 時, 令
時, 令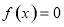 , 即
, 即 , 解得
, 解得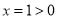 .
.
∴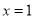 是函數
是函數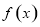 的一個零點. 6分
的一個零點. 6分
(ⅱ)當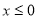 時, 令
時, 令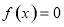 , 即
, 即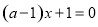 .(※)
.(※)
①當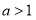 時, 由(※)得
時, 由(※)得 ,∴
,∴ 是函數
是函數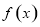 的一個零點; 8分
的一個零點; 8分
②當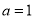 時, 方程(※)無解;
時, 方程(※)無解;
③當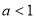 時, 由(※)得
時, 由(※)得 ,(不合題意,舍去) 10分
,(不合題意,舍去) 10分
綜上, 當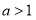 時, 函數
時, 函數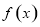 的零點是
的零點是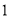 和
和 ;
;
當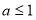 時, 函數
時, 函數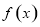 的零點是
的零點是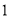 . 12分
. 12分
考點:1.函數單調性的判斷與證明;2.分段函數的解析式求法及其圖象的作法;3.函數的零點.


科目:高中數學 來源:2016屆浙江省杭州市高一上學期抽測數學試卷(解析版) 題型:選擇題
下列函數 中,滿足“對任意
中,滿足“對任意 ,
,
 (0,
(0, ),當
),當 <
< 時,
時, >
> 的是 ( )
的是 ( )
(A)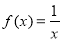 (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中數學 來源:2016屆河南省鄭州市高一上學期期末考試數學試卷(解析版) 題型:解答題
如圖,一個圓錐形的空杯子上面放著一個半球形的冰淇淋,如果冰淇淋融化了并流入杯中,會溢出杯子嗎?請用你的計算數據說明理由。(冰、水的體積差異忽略不計)

查看答案和解析>>
科目:高中數學 來源:2016屆河南周口市英文學校高一上學期第三次月考數學試卷(解析版) 題型:填空題
根據統計,一名工人組裝第 件某產品所用的時間(單位:分鐘)為
件某產品所用的時間(單位:分鐘)為 (
( 為常數).已知工人組裝第4件產品用時30分鐘,組裝第A件產品用時15分鐘,那么c和A的值分別是 .
為常數).已知工人組裝第4件產品用時30分鐘,組裝第A件產品用時15分鐘,那么c和A的值分別是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com