
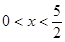 ,求
,求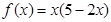 的最大值。
的最大值。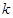 為何值時,直線
為何值時,直線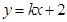 和曲線
和曲線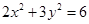 有兩個公共點。
有兩個公共點。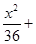
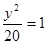 ;(2)點P的坐標為
;(2)點P的坐標為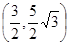 ;
;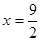 時,d取最小值
時,d取最小值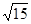 。
。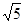 ,半焦距c1=
,半焦距c1=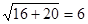 ,
,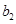 =
=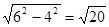 ,
,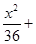
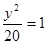 …………4分
…………4分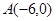 ,
,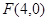 ,設點P的坐標為
,設點P的坐標為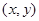 ,則
,則 由已知得
由已知得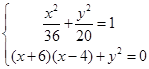 …………6分
…………6分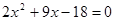 ,解之得
,解之得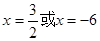 ,
, 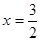 ,于是
,于是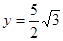 ,所以點P的坐標為
,所以點P的坐標為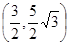 ……8分
……8分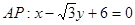 ,設點M是
,設點M是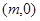 ,則點M到直線AP的距離是
,則點M到直線AP的距離是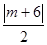 ,于是
,于是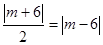 ,
,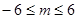
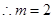 …………10分
…………10分 時,橢圓上的點到
時,橢圓上的點到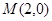 的距離
的距離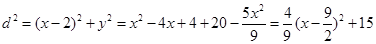
 ∴當
∴當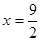 時,d取最小值
時,d取最小值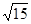 …………12分
…………12分

 計算高手系列答案
計算高手系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com