
【題目】如圖,菱形![]() 與正
與正![]() 所在平面互相垂直,
所在平面互相垂直,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
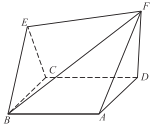
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明過程詳見解析(2)![]()
【解析】
(1)過點![]() 作
作![]() 于
于![]() ,由面面垂直的性質可知
,由面面垂直的性質可知![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,可得
,可得![]() ,即四邊形
,即四邊形![]() 為平行四邊形,得到線線平行,從而得到線面平行;
為平行四邊形,得到線線平行,從而得到線面平行;
(2)分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,求出平面
,求出平面![]() 的法向量,利用線面角的向量公式進行計算即可得到答案.
的法向量,利用線面角的向量公式進行計算即可得到答案.
解:(1)如圖,過點![]() 作
作![]() 于
于![]() ,連接EH,∴
,連接EH,∴![]() .
.
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() 于
于![]() ∴
∴ ![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,![]() .∴
.∴![]() ,
,
∴四邊形![]() 為平行四邊形. ∴
為平行四邊形. ∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)連接![]() .由(1)得
.由(1)得![]() 為
為![]() 中點,又
中點,又![]() ,
,![]() 為等邊三角形,
為等邊三角形,
∴![]() .分別以
.分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸建立
軸建立
如圖所示的空間直角坐標系![]() .
.

![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]()
![]() ,
,
設平面![]() 的法向量為
的法向量為![]() .
.
由 ,得
,得
令![]() ,得
,得![]() .
.
![]() ,
,
直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】某地區有小學21所,中學14所,大學7所,現采取分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查。
(I)求應從小學、中學、大學中分別抽取的學校數目。
(II)若從抽取的6所學校中隨機抽取2所學校做進一步數據分析,
(1)列出所有可能的抽取結果;
(2)求抽取的2所學校均為小學的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有工人1000名,其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人).現用分層抽樣方法(按A類,B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(生產能力指一天加工的零件數)
(1)A類工人中和B類工人各抽查多少工人?
(2)從A類工人中抽查結果和從B類工人中的抽查結果分別如下表1和表2:
表1:
生產能力分組 |
|
|
|
|
|
人數 | 4 | 8 | x | 5 | 3 |
表2:
生產能力分組 |
|
|
|
|
人數 | 6 | y | 36 | 18 |
①先確定x,y,再在答題紙上完成下列頻率分布直方圖.就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)
②分別估計A類工人和B類工人生產能力的平均數,并估計該工廠工人和生產能力的平均數(同一組中的數據用該區間的中點值作代表)

圖1A類工人生產能力的頻率分布直方圖 圖2B類工人生產能力的頻率分布直方圖
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】各國醫療科研機構都在研制某種病毒疫苗,現有G,E,F三個獨立的醫療科研機構,它們在一定時期內能研制出疫苗的概率分別是![]() .求:
.求:
(1)他們都研制出疫苗的概率;
(2)他們都失敗的概率;
(3)他們能夠研制出疫苗的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】企業需為員工繳納社會保險,繳費標準是根據職工本人上一年度月平均工資(單位:元)的![]() 繳納,
繳納,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企業員工甲在2014年至2018年各年中每月所撒納的養老保險數額y(單位:元)與年份序號t的統計如下表:
(1)求出t關于t的線性回歸方程![]() ;
;
(2)試預測2019年該員工的月平均工資為多少元?
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
(注: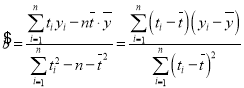 ,
,![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”.其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語文描述:在羨除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,兩條平行線
,兩條平行線![]() 與
與![]() 間的距離為
間的距離為![]() ,直線
,直線![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則該羨除的體積為
,則該羨除的體積為![]() .已知某羨除的三視圖如圖所示,則該羨除的體積為
.已知某羨除的三視圖如圖所示,則該羨除的體積為

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,定點
,定點![]() ,
,![]() 為圓上任意一點,線段
為圓上任意一點,線段![]() 的垂直平分線
的垂直平分線![]() 和半徑
和半徑![]() 相交于點
相交于點![]() ,當點
,當點![]() 在圓上運動時,點
在圓上運動時,點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若過定點![]() 的直線交曲線
的直線交曲線![]() 于不同的兩點
于不同的兩點![]() ,
,![]() (點
(點![]() 在點
在點![]() ,
,![]() 之間),且滿足
之間),且滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對數函數g(x)=1ogax(a>0,a≠1)和指數函數f(x)=ax(a>0,a≠1)互為反函數.已知函數f(x)=3x,其反函數為y=g(x).
(Ⅰ)若函數g(kx2+2x+1)的定義域為R,求實數k的取值范圍;
(Ⅱ)若0<x1<x2且|g(x1)|=|g(x2)|,求4x1+x2的最小值;
(Ⅲ)定義在I上的函數F(x),如果滿足:對任意x∈I,總存在常數M>0,都有-M≤F(x)≤M成立,則稱函數F(x)是I上的有界函數,其中M為函數F(x)的上界.若函數h(x)=![]() ,當m≠0時,探求函數h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范圍,若不存在,請說明理由.
,當m≠0時,探求函數h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范圍,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com