
已知 (
( )
)
(1)若方程 有3個不同的根,求實數
有3個不同的根,求實數 的取值范圍;
的取值范圍;
(2)在(1)的條件下,是否存在實數 ,使得
,使得 在
在 上恰有兩個極值點
上恰有兩個極值點 ,且滿足
,且滿足 ,若存在,求實數
,若存在,求實數 的值,若不存在,說明理由.
的值,若不存在,說明理由.
(1) ;(2)不存在,參考解析
;(2)不存在,參考解析
解析試題分析:(1)由已知 (
( ),若方程
),若方程 有3個不同的根,則可得到
有3個不同的根,則可得到 或
或 對兩個方程分別討論即可到結論.
對兩個方程分別討論即可到結論.
(2)在(1)的條件下,是否存在實數 ,使得
,使得 在
在 上恰有兩個極值點
上恰有兩個極值點 ,通過對函數求導,判斷導函數的根的情況,通過換元使得等式簡潔些.要滿足
,通過對函數求導,判斷導函數的根的情況,通過換元使得等式簡潔些.要滿足 ,由于
,由于 ,所以可得
,所以可得 ,通過驗證根是否存在.即可得到結論.
,通過驗證根是否存在.即可得到結論.
(1)解:由 得:
得: 或
或
可得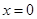 或
或 且
且
∵方程 有3個不同的根,
有3個不同的根,
∴方程 有兩個不同的根
有兩個不同的根
∴
又∵ ,且要保證
,且要保證 能取到0∴
能取到0∴ 即
即
∴ .
.
(2)解:∵
令 ,設
,設
∴
 ∵
∵ ∴
∴ ∴
∴


∵ ∴
∴ ,
, ∴
∴
∴存在 ,使得
,使得 ,另外有
,另外有 ,使得
,使得
假設存在實數 ,使得
,使得 在
在 上恰有兩個極值點
上恰有兩個極值點 ,且滿足
,且滿足
則存在 ,使得
,使得 ,另外有
,另外有 ,即
,即
∴ ,∴
,∴ ,即
,即
即 (*)
(*)
設
∴
∵ ∴
∴
∴ ∴
∴ 在
在 上是增函數
上是增函數
∴


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
設函數f(x)=x+ 的圖象為C1,C1關于點A(2,1)對稱的圖象為C2,C2對應的函數為g(x).
的圖象為C1,C1關于點A(2,1)對稱的圖象為C2,C2對應的函數為g(x).
(1)求g(x)的解析式;
(2)若直線y=m與C2只有一個交點,求m的值和交點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•重慶)某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度).設該蓄水池的底面半徑為r米,高為h米,體積為V立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12000π元(π為圓周率).
(1)將V表示成r的函數V(r),并求該函數的定義域;
(2)討論函數V(r)的單調性,并確定r和h為何值時該蓄水池的體積最大.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某幼兒園準備建一個轉盤,轉盤的外圍是一個周長為k米的圓.在這個圓上安裝座位,且每個座位和圓心處的支點都有一根直的鋼管相連經預算,轉盤上的每個座位與支點相連的鋼管的費用為3k元/根,且當兩相鄰的座位之間的圓弧長為x米時,相鄰兩座位之間的鋼管和其中一個座位的總費用為 k元.假設座位等距分布,且至少有兩個座位,所有座位都視為點,且不考慮其他因素,記轉盤的總造價為y元.
k元.假設座位等距分布,且至少有兩個座位,所有座位都視為點,且不考慮其他因素,記轉盤的總造價為y元.
(1)試寫出y關于x的函數關系式,并寫出定義域;
(2)當k=50米時,試確定座位的個數,使得總造價最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com