
【題目】已知下圖中,四邊形 ABCD是等腰梯形, ![]() ,
, ![]() ,O、Q分別為線段AB、CD的中點,OQ與EF的交點為P,OP=1,PQ=2,現(xiàn)將梯形ABCD沿EF折起,使得
,O、Q分別為線段AB、CD的中點,OQ與EF的交點為P,OP=1,PQ=2,現(xiàn)將梯形ABCD沿EF折起,使得![]() ,連結AD、BC,得一幾何體如圖所示.
,連結AD、BC,得一幾何體如圖所示.
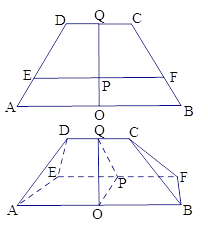
(Ⅰ)證明:平面ABCD![]() 平面ABFE;
平面ABFE;
(Ⅱ)若上圖中, ![]() ,CD=2,求平面ADE與平面BCF所成銳二面角的余弦值.
,CD=2,求平面ADE與平面BCF所成銳二面角的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)先根據(jù)![]() ,
, ![]() 得
得![]() ⊥平面
⊥平面![]() ,故
,故![]() ,結合勾股定理
,結合勾股定理![]() ,由線面垂直判定定理可得
,由線面垂直判定定理可得![]()
![]() 平面
平面![]() ,由面面垂直判定定理可得結論;(2)以
,由面面垂直判定定理可得結論;(2)以![]() 為原點,
為原點, ![]() 所在的直線為
所在的直線為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,可求得面
,可求得面![]() 的一個法向量
的一個法向量![]() ,面
,面![]() 的一個法向量
的一個法向量![]() ,求出向量夾角即可.
,求出向量夾角即可.
試題解析: (1)證明:在圖中,四邊形![]() 為等腰梯形,
為等腰梯形, ![]() 分別為線段
分別為線段![]() 的中點,
的中點,
∴![]() 為等腰梯形
為等腰梯形![]() 的對稱軸,又
的對稱軸,又![]() //
// ![]() ,
,
∴![]() 、
、![]() ,①
,①
在圖中,∵![]() ,∴
,∴![]()
由①及![]() ,得
,得![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
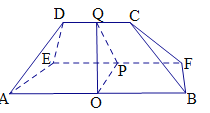
(2)在圖中,由![]() ,
, ![]() ,易得
,易得![]() ,
, ![]() ,
,
以![]() 為原點,
為原點, ![]() 所在的直線為
所在的直線為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,如圖所示,
,如圖所示,
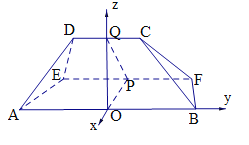
則![]() 、
、![]() 、
、![]()
得![]() ,
, ![]()
設![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
則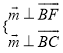 ,得
,得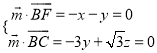 ,
,
取![]() ,得
,得![]()
同理可得平面![]() 的一個法向量
的一個法向量![]()
設所求銳二面角的平面角為![]() ,
,
則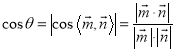 =
=![]()
所以平面ADE與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】設關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是從0,1,2,3四個數(shù)中任取的一個數(shù),
是從0,1,2,3四個數(shù)中任取的一個數(shù), ![]() 是從0,1,2三個數(shù)中任取的一個數(shù),求上述方程有實根的概率;
是從0,1,2三個數(shù)中任取的一個數(shù),求上述方程有實根的概率;
(2)若![]() 時從區(qū)間
時從區(qū)間![]() 上任取的一個數(shù),
上任取的一個數(shù), ![]() 是從區(qū)間
是從區(qū)間![]() 上任取的一個數(shù),求上述方程有實根的概率.
上任取的一個數(shù),求上述方程有實根的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可為一個三角形的三邊長,則稱函數(shù)
均可為一個三角形的三邊長,則稱函數(shù)![]() 為“三角形函數(shù)”.已知函數(shù)
為“三角形函數(shù)”.已知函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是“三角形函數(shù)”,則實數(shù)
上是“三角形函數(shù)”,則實數(shù)![]() 的取值范圍為( )
的取值范圍為( )
A. 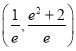 B.
B. ![]()
C. ![]() D.
D. 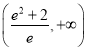
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 與拋物線
與拋物線![]() 共焦點
共焦點![]() ,拋物線上的點M到y軸的距離等于
,拋物線上的點M到y軸的距離等于![]() ,且橢圓與拋物線的交點Q滿足
,且橢圓與拋物線的交點Q滿足![]() .
.
(I)求拋物線的方程和橢圓的方程;
(II)過拋物線上的點![]() 作拋物線的切線
作拋物線的切線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點,求此切線在x軸上的截距的取值范圍.
兩點,求此切線在x軸上的截距的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某舉重運動隊為了解隊員的體重分布情況,從50名隊員中抽取10名作調查.抽取時現(xiàn)將全體隊員隨機按1~50編號,并按編號順序平均分成10組,每組抽一名,且各組內抽取的編號依次增加5進行系統(tǒng)抽樣.
(1)若第5組抽出的號碼為22,寫出所有被抽取出來的編號;
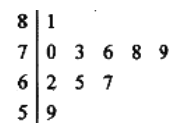
(2)分別統(tǒng)計被抽取的10名隊員的體重(單位:公斤),獲得如圖所示的體重數(shù)據(jù)的莖葉圖,根據(jù)莖葉圖求該樣本的平均數(shù)和中位數(shù);
(3)在題(2)的莖葉圖中,從題中不輕于73公斤的隊員中隨機抽取2名隊員的體重數(shù)據(jù),求體重為81公斤的隊員被抽到的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分組的頻率分布直方圖如圖所示.
分組的頻率分布直方圖如圖所示.
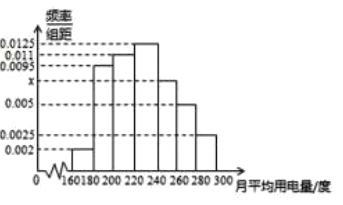
(1)求直方圖中![]() 的值;
的值;
(2)求月平均用電量的眾數(shù)和中位數(shù);
(3)在月平均用電量在![]() ,
, ![]() ,
, ![]() 的三組用戶中,用分層抽樣的方法抽取10戶居民,則月平均用電量在
的三組用戶中,用分層抽樣的方法抽取10戶居民,則月平均用電量在![]() 的用戶中應抽取多少戶?
的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,已知曲線
中,已知曲線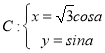 (
(![]() 為參數(shù)),在以原點
為參數(shù)),在以原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立的極坐標系中,直線的極坐標方程為:
軸的非負半軸為極軸建立的極坐標系中,直線的極坐標方程為: ![]() .
.
(Ⅰ)求曲線![]() 的普通方程和直線的直角坐標方程;
的普通方程和直線的直角坐標方程;
(Ⅱ)過點![]() 且與直線平行的直線
且與直線平行的直線![]() 交
交![]() 于
于![]() ,
, ![]() 兩點,求點
兩點,求點![]() 到
到![]() ,
, ![]() 兩點的距離之積.
兩點的距離之積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,順次連接橢圓
,順次連接橢圓![]() 的四個頂點得到的四邊形的面積為16.
的四個頂點得到的四邊形的面積為16.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過橢圓![]() 的頂點
的頂點![]() 的直線
的直線![]() 交橢圓于另一點
交橢圓于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,若
,若![]() 、
、![]() 、
、![]() 成等比數(shù)列,求直線
成等比數(shù)列,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() .
.
(Ⅰ)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(Ⅱ)若橢圓![]() 的短軸長為
的短軸長為![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com