Question

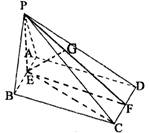
（08年惠州一中三模理） 如圖，四棱錐P―ABCD的底面是AB=2，BC=的矩形，側面PAB是等邊三角形，且側面PAB⊥底面ABCD

   （I）證明：側面PAB⊥側面PBC；

   （II）求側棱PC與底面ABCD所成的角；

 （III）求直線AB與平面PCD的距離．

 

Answer 1

解析：（I）證明：在矩形ABCD中，BC⊥AB

         又∵面PAB⊥底面ABCD側面PAB∩底面ABCD=AB

         ∴BC⊥側面PAB       又∵BC側面PBC

         ∴側面PAB⊥側面PBC）

  （II）解：取AB中點E，連結PE、CE

         又∵△PAB是等邊三角形   ∴PE⊥AB 

         又∵側面PAB⊥底面ABCD，∴PE⊥面ABCD

         ∴∠PCE為側棱PC與底面ABCD所成角

        

         在Rt△PEC中，∠PCE=45°為所求

   （Ⅲ）解：在矩形ABCD中，AB//CD

         ∵CD側面PCD，AB側面PCD，∴AB//側面PCD

         取CD中點F，連EF、PF，則EF⊥AB

         又∵PE⊥AB    ∴AB⊥平面PEF   又∵AB//CD

         ∴CD⊥平面PEF   ∴平面PCD⊥平面PEF

         作EG⊥PF，垂足為G，則EC⊥平面PCD

         在Rt△PEF中，EG=為所求.