【題目】已知橢圓
的一個焦點在直線
上，且離心率
.
（1）求該橢圓的方程；
（2）若
與
是該橢圓上不同的兩點，且線段
的中點
在直線
上，試證： 
軸上存在定點
，對于所有滿足條件的
與
，恒有
；
【答案】（1）
（2）見解析
【解析】試題分析：（1）利用橢圓的性質(zhì)、離心率計算公式
及焦點即可得方程；
（2）當直線
的斜率存在時，設(shè)直線
的方程為
，與橢圓聯(lián)立得
，設(shè)
，由線段
的中點
在直線
上，得
，假設(shè)在
軸上存在定點
， 
，進而得
，即可求得
，當直線
的斜率不存在時，易得成立.
試題解析：
（1）∵橢圓
的一個焦點在直線
上，∴
，
又
，∴
，
∴該橢圓的方程為
.
（2）當直線
的斜率存在時，設(shè)直線
的方程為
，
，
，
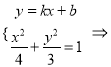
設(shè)
，則
， 
，
∵弦
的中點
在直線
上，∴
，
∴
，∴
，
將
代入
得
，
假設(shè)在
軸上存在定點
， 
，
∴
，
∴
，即
，
當直線
的斜率不存在時，直線
垂直于
軸，此時
顯然成立，綜上， 
軸上存在定點
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左右焦點分別是
，橢圓C的上頂點到直線
的距離為
，過
且垂直于x軸的直線與橢圓C相交于M，N兩點，
且｜MN｜＝1。
（I）求橢圓
的方程；
（II）過點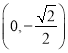
的直線與橢圓C相交于P，Q兩點，點
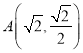），且
，求直線
的方程。
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
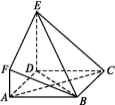
(1)求二面角F-BE-D的余弦值;
(2)設(shè)點M是線段BD上一個動點,試確定點M的位置,使得AM∥平面BEF,并證明你的結(jié)論.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某研究機構(gòu)對某校高二文科學(xué)生的記憶力x和判斷力y進行統(tǒng)計分析，得下表數(shù)據(jù)．
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
參考公式：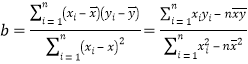
(1)請畫出上表數(shù)據(jù)的散點圖；
(2)請根據(jù)上表提供的數(shù)據(jù)，用最小二乘法求出y關(guān)于x的線性回歸方程；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列說法錯誤的是
A. 對分類變量X與Y，隨機變量K2的觀測值k越大，則判斷“X與Y有關(guān)系”的把握程度越小
B. 在回歸直線方程
=0.2x+0.8中，當解釋變量x每增加1個單位時，預(yù)報變量
平均增加0.2個單位
C. 兩個隨機變量的線性相關(guān)性越強，則相關(guān)系數(shù)的絕對值就越接近于1
D. 回歸直線過樣本點的中心（
， 
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為研究某種圖書每冊的成本費
（元）與印刷數(shù)
（千冊）的關(guān)系，收集了一些數(shù)據(jù)并作了初步處理，得到了下面的散點圖及一些統(tǒng)計量的值．
|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中
， 
．
（1）根據(jù)散點圖判斷： 
與
哪一個更適宜作為每冊成本費
（元）與印刷數(shù)
（千冊）的回歸方程類型？（只要求給出判斷，不必說明理由）
（2）根據(jù)（1）的判斷結(jié)果及表中數(shù)據(jù)，建立
關(guān)于
的回歸方程（回歸系數(shù)的結(jié)果精確到0.01）；
（3）若每冊書定價為10元，則至少應(yīng)該印刷多少冊才能使銷售利潤不低于78840元？（假設(shè)能夠全部售出，結(jié)果精確到1）
（附：對于一組數(shù)據(jù)
， 
，…， 
，其回歸直線
的斜率和截距的最小二乘估計分別為
， 
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
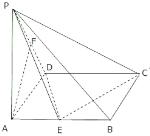
【題目】已知四棱錐
﹣
中，底面ABCD是矩形，
⊥平面，
，
是
的中點，
是線段
上的點．
(1)當是的中點時，求證：
∥平面
．
(2)當
：
= 2：1時，求二面角﹣
﹣
的余弦值．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
