Question

已知數列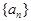是等差數列，且，，
（1）求數列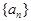的通項公式； （2）令，求數列前n項和.

Answer 1

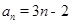（1）（2）

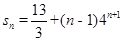
解析試題分析：解：（1）數列{a_n}是等差數列，且a₁=1，a₁+a₂+a₃=12，設出公差為d，∴a₁+a₁+d+a₁+2d=12，∴a₁+d=4，可得2+d=4，解得d=2，∴a_n=a₁+（n-1）d=1+（n-1）×2=2n+1，（2）數列{a_n}的通項公式為a_n=n•2ⁿ，設其前n項和為S_n，∴S_n=1•2¹+2•2²+3•2³+…+n•2ⁿ①
2S_n=1•2²+2•2³+3•2⁴+…+n•2ⁿ⁺¹②
①-②可得-S_n=2¹+2²+2³+…+2ⁿ-n•2ⁿ⁺¹②
∴-S_n=-2+2²⁺2³++…+2ⁿ -n•2ⁿ⁺¹，
∴S_n=n×2ⁿ⁺¹-2ⁿ⁺¹+2=（n-1）2ⁿ⁺¹+2；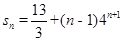

考點：等差數列，數列的求和
點評：主要是考查了等差數列的定義，以及通項公式的運用，以及錯位相減法來求解數列的和，屬于中檔題。