
【題目】以下資料是一位銷售經理收集到的每年銷售額y(千元)和銷售經驗x(年)的關系:
銷售經驗x/年 | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
年銷售額y/千元 | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)依據這些數據畫出散點圖并作直線![]() =78+4.2x,計算
=78+4.2x,計算![]() ;
;
(2)依據這些數據求回歸直線方程并據此計算![]() ;
;
(3)比較(1) (2)中的殘差平方和![]() 的大小.
的大小.
【答案】(1)179.28; (2)![]() =80+4x; (3)(2)較小.
=80+4x; (3)(2)較小.
【解析】
對于(1),首先根據題目信息在坐標系中標出點,在連接即可得到散點圖與直線y=78++4.2x,再根據x=1,3,…,13,得到![]() 的值代入計算即可得到答案;
的值代入計算即可得到答案;
對于(2)、(3),首先根據線性回歸方程恒過樣本中心點的性質,計算![]() 、
、![]() 的值,再根據
的值,再根據![]() 、
、![]() 的計算公式進行計算即可得到回歸方程,再根據此方程令x=1,3,…,13,得到
的計算公式進行計算即可得到回歸方程,再根據此方程令x=1,3,…,13,得到![]() 的值,代入計算即可得到
的值,代入計算即可得到![]() ,將其與(1)中的值比較即可得到答案.
,將其與(1)中的值比較即可得到答案.
(1)散點圖與直線![]() =78+4.2x的圖形如圖,
=78+4.2x的圖形如圖,
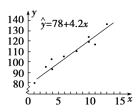 ,
,
對x=1,3,…,13,有
![]() i=82.2,90.6,94.8,94.8,103.2,111.6,120,120,124.2,132.6,
i=82.2,90.6,94.8,94.8,103.2,111.6,120,120,124.2,132.6,![]() =179.28.
=179.28.
(2)![]() =
=![]()
![]() ,
,![]()
∴![]() =
=![]() =4,
=4,![]() =
=![]() -
-![]()
![]() =108-7×4=80,
=108-7×4=80,
故![]() =80+4x.
=80+4x.
(3)對x=1,3,…,13,有
![]() =84,92,96,96,104,112,120,120,124,132,即
=84,92,96,96,104,112,120,120,124,132,即![]() 較小.
較小.


科目:高中數學 來源: 題型:
【題目】在心理學研究中,常采用對比試驗的方法評價不同心理暗示對人的影響,具體方法如下:將參加試驗的志愿者隨機分成兩組,一組接受甲種心理暗示,另一組接受乙種心理暗示,通過對比這兩組志愿者接受心理暗示后的結果來評價兩種心理暗示的作用,現有6名男志愿者A1 , A2 , A3 , A4 , A5 , A6和4名女志愿者B1 , B2 , B3 , B4 , 從中隨機抽取5人接受甲種心理暗示,另5人接受乙種心理暗示.(12分)
(Ⅰ)求接受甲種心理暗示的志愿者中包含A1但不包含B1的概率.
(Ⅱ)用X表示接受乙種心理暗示的女志愿者人數,求X的分布列與數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(sin(x+
=(sin(x+ ![]() ),1),
),1), ![]() =(4,4cosx﹣
=(4,4cosx﹣ ![]() )
)
(1)若 ![]() ⊥
⊥ ![]() ,求sin(x+
,求sin(x+ ![]() )的值;
)的值;
(2)設f(x)= ![]()
![]() ,若α∈[0,
,若α∈[0, ![]() ],f(α﹣
],f(α﹣ ![]() )=2
)=2 ![]() ,求cosα的值.
,求cosα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某書店共有韓寒的圖書6種,其中價格為25元的有2種,18元的有3種,16元的有1種.書店若把這6種韓寒的圖書打包出售,據統計每套的售價與每天的銷售數量如下表所示:
售價x/元 | 105 | 108 | 110 | 112 |
銷售數量y/套 | 40 | 30 | 25 | 15 |
(1)根據上表,利用最小二乘法得到回歸直線方程![]() ,求
,求![]() ;
;
(2)若售價為100元,則每天銷售的套數約為多少(結果保留到整數)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知過點![]() 的直線
的直線![]() 的參數方程是
的參數方程是 (
(![]() 為參數).以平面直角坐標系的原點為極點,
為參數).以平面直角坐標系的原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程式為
的極坐標方程式為![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設復數z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在復平面內對應的點在第一象限,且z=-3+4i.
(1)求z2及|z2|.
(2)若z1=z2,求θ與a2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中社團進行社會實踐,對![]() 歲的人群隨機抽取n人進行了一次是否開通“微博”的調查,若開通“微博”的稱為“時尚族”,否則稱為“非時尚族”,通過調查分別得到如圖所示統計表和各年齡段人數頻率分布直方圖:
歲的人群隨機抽取n人進行了一次是否開通“微博”的調查,若開通“微博”的稱為“時尚族”,否則稱為“非時尚族”,通過調查分別得到如圖所示統計表和各年齡段人數頻率分布直方圖:
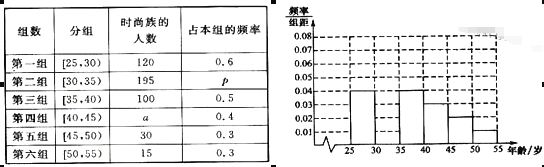
完成以下問題:
(Ⅰ)補全頻率分布直方圖并求![]() 的值;
的值;
(Ⅱ)從![]() 歲年齡段的“時尚族”中采用分層抽樣法抽取
歲年齡段的“時尚族”中采用分層抽樣法抽取![]() 人參加網絡時尚達人大賽,其中選取
人參加網絡時尚達人大賽,其中選取![]() 人作為領隊,記選取的
人作為領隊,記選取的![]() 名領隊中年齡在
名領隊中年齡在![]() 歲的人數為
歲的人數為![]() ,求
,求![]() 的分布列
的分布列
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com