
(1)求點P的軌跡方程C;
(2)若曲線C為焦點在x軸上的橢圓,試求實數t的取值范圍;
(3)若t=2,點M、N是C上關于原點對稱的兩個動點,點Q的坐標為(![]() ,3),求△QMN的面積S的最大值.
,3),求△QMN的面積S的最大值.
解:(1)設點A(a,0),B(0,b),P(x,y),∵![]() =t
=t![]() ,即(x-a,y)=t(-x,b-y),即
,即(x-a,y)=t(-x,b-y),即![]()
則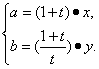 又∵|AB|=2,即a2+b2=4,∴
又∵|AB|=2,即a2+b2=4,∴![]() +
+![]() =1.
=1.
∴點P的軌跡方程C: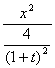 +
+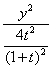 =1.
=1.
(2)∵曲線C為焦點在x軸上的橢圓,∴![]() >
>![]() ,得t2<1
,得t2<1![]() -1<t<1.
-1<t<1.
又∵t>0,∴0<t<1.
(3)當t=2時,曲線C的方程為![]() +
+![]() =1.
=1.
設M(x1,y1),N(-x1,-y1),則|MN|=2![]() .
.
當x1≠0時,設直線MN的方程為y=![]() x,則點Q到直線MN的距離h=
x,則點Q到直線MN的距離h=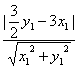 ,
,
∴△QMN的面積S=![]() ·2
·2![]() ·
·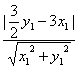 =|
=|![]() y1-3x1|.
y1-3x1|.
∴S2=|![]() y1-3x1|2=9x12+
y1-3x1|2=9x12+![]() y12-9x1y1.又∵
y12-9x1y1.又∵![]() +
+![]() =1,∴9x12+
=1,∴9x12+![]() y12=4.
y12=4.
∴S2=4-9x1y1.而1=![]() +
+![]() ≥-2·
≥-2·![]() ·
·![]() =
=![]() ,
,
則-9x1y1≤4,即S2≤8,S≤2![]() .當且僅當
.當且僅當![]() =
=![]() ,即x1=
,即x1=![]() y1時,“=”成立.
y1時,“=”成立.
當x1=0時,|MN|=![]() ,△QMN的面積S=
,△QMN的面積S=![]() ×
×![]() ×
×![]() =2.∴S的最大值是2
=2.∴S的最大值是2![]() .
.


科目:高中數學 來源: 題型:
| AP |
| PB |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
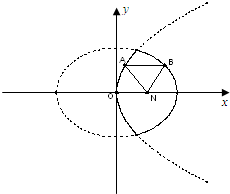 [理]如圖,已知動點A,B分別在圖中拋物線y2=4x及橢圓
[理]如圖,已知動點A,B分別在圖中拋物線y2=4x及橢圓| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
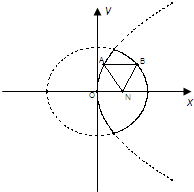 已知動點A、B分別在圖中拋物線y2=4x及橢圓
已知動點A、B分別在圖中拋物線y2=4x及橢圓| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知動點A、B分別在圖中拋物線y2=4x及橢圓
已知動點A、B分別在圖中拋物線y2=4x及橢圓| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2011-2012年福建省四地六校高二第二次月考理科數學 題型:選擇題
已知動點A、B分別在圖中拋物線 及橢圓
及橢圓
 的實線上運動,若
的實線上運動,若 ∥
∥ 軸,點N的坐標
軸,點N的坐標
為(1,0),則三角形ABN的周長 的取值范圍是 ( )
的取值范圍是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com