
已知數列 滿足
滿足 ,
,
(1)若 ,求
,求 ;
;
(2)是否存在 ,使當
,使當 時,
時, 恒為常數.若存在求
恒為常數.若存在求 ,否則說明理由;
,否則說明理由;
(1)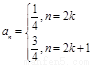 其中
其中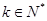
(2)存在三組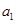 和
和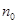 :
:
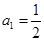 時,
時,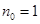 ;
; 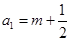 時,
時,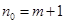 ;
;
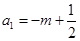 時,
時, 其中
其中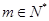
【解析】(1)根據遞推關系可由a1,分別求出a2,a3,a4,然后歸納出an的通項公式.
(2)本小題難度偏大,應從特值出發探索,做此類問題應有較強的計算能力,邏輯分析能力,和扎實的數學基本功,還要有堅強的意志.
解:(1)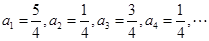 2分
2分
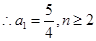 時,
時,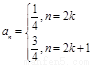 ,其中
,其中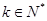 ` ………….6分
` ………….6分
(2)因為存在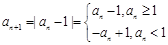 ,所以當
,所以當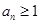 時,
時,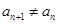
①若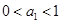 ,則
,則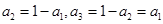 ,此時只需:
,此時只需: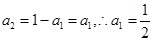
故存在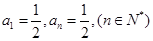 ……………..8分
……………..8分
②若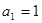 不符合題
不符合題 意………………9分
意………………9分
③若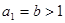 ,不妨設
,不妨設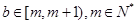 ,易知
,易知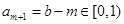 ,
,
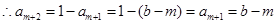
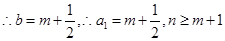 時,
時,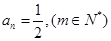 …………….11分
…………….11分
④若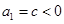 ,不妨設
,不妨設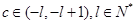 ,易知
,易知
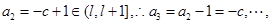
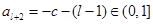
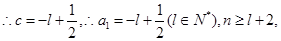 則
則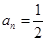 ………..13分
………..13分
故存在三組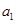 和
和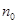 :
:
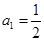 時,
時,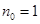 ;
; 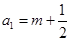 時,
時,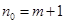 ;
;
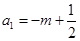 時,
時, 其中
其中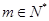 …………14分
…………14分


科目:高中數學 來源:2014屆陜西省高二上學期期末考試理科數學試卷(解析版) 題型:解答題
已知數列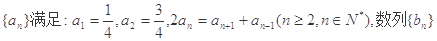 滿足:
滿足: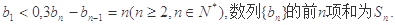
(1)求證:數列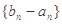 為等比數列;
為等比數列;
(2)求證:數列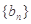 為遞增數列;
為遞增數列;
(3)若當且僅當 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省南通市高三第二次模擬考試數學試題 題型:解答題
已知數列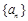 滿足
滿足 .
.
(1)求數列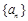 的通項公式;
的通項公式;
(2)對任意給定的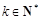 ,是否存在
,是否存在 (
(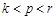 )使
)使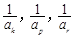 成等差數列?若存
成等差數列?若存
在,用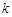 分別表示
分別表示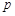 和
和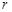 (只要寫出一組);若不存在,請說明理由;
(只要寫出一組);若不存在,請說明理由;
(3)證明:存在無窮多個三邊成等比數列且互不相似的三角形,其邊長為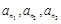 .
.
查看答案和解析>>
科目:高中數學 來源:2010年湖北省高二12月月考數學試卷 題型:解答題
已知數列 滿足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
滿足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
(1)求a2、a3
(2)猜想 的表達式,并用數學歸納法證明你的結論
的表達式,并用數學歸納法證明你的結論
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省高二下學期期中考試數學(理) 題型:解答題
(14分)已知數列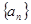 滿足
滿足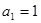 ,
,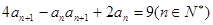
(1)求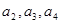 。(2)由(1)猜想
。(2)由(1)猜想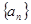 的通項公式。(3)用數學歸納法證明(2)的結果。[來源:學#科#網]
的通項公式。(3)用數學歸納法證明(2)的結果。[來源:學#科#網]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com