
【題目】三棱錐A﹣BCD及其側(cè)視圖、俯視圖如圖所示,設M,N分別為線段AD,AB的中點,P為線段BC上的點,且MN⊥NP. 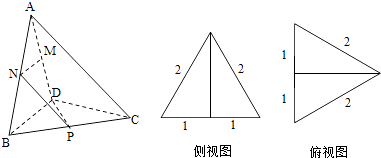
(1)證明:P是線段BC的中點;
(2)求二面角A﹣NP﹣M的余弦值.
【答案】
(1)證明:由三棱錐A﹣BCD及其側(cè)視圖、俯視圖可知,在三棱錐A﹣BCD中:
平面ABD⊥平面CBD,AB=AD=BD=CD=CB=2
設O為BD的中點,連接OA,OC
于是OA⊥BD,OC⊥BD 所以BD⊥平面OACBD⊥AC
因為M,N分別為線段AD,AB的中點,所以MN∥BD,MN⊥NP,故BD⊥NP
假設P不是線段BC的中點,則直線NP與直線AC是平面ABC內(nèi)相交直線
從而BD⊥平面ABC,這與∠DBC=60°矛盾,所以P為線段BC的中點
(2)解:以O為坐標原點,OB,OC,OA分別為x,y,z軸建立空間直角坐標系,
則A(0,0, ![]() ),M(
),M( ![]() ,O,
,O, ![]() ),N(
),N( ![]() ,0,
,0, ![]() ),P(
),P( ![]() ,
, ![]() ,0)
,0)
于是 ![]() ,
, ![]() ,
, ![]()
設平面ANP和平面NPM的法向量分別為 ![]() 和
和 ![]()
由 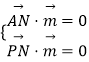 ,則
,則 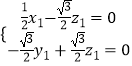 ,設z1=1,則
,設z1=1,則 ![]()
由 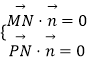 ,則
,則 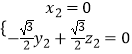 ,設z2=1,則
,設z2=1,則 ![]()
cos ![]() =
= ![]() =
= ![]() =
= ![]()
所以二面角A﹣NP﹣M的余弦值 ![]()
【解析】(1)用線面垂直的性質(zhì)和反證法推出結(jié)論,(2)先建空間直角坐標系,再求平面的法向量,即可求出二面角A﹣NP﹣M的余弦值.
【考點精析】解答此題的關(guān)鍵在于理解直線與平面平行的判定的相關(guān)知識,掌握平面外一條直線與此平面內(nèi)的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案科目:高中數(shù)學 來源: 題型:
【題目】記max{x,y}= ![]() ,min{x,y}=
,min{x,y}= ![]() ,設
,設 ![]() ,
, ![]() 為平面向量,則( )
為平面向量,則( )
A.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≤min{|
|}≤min{| ![]() |,|
|,| ![]() |}
|}
B.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≥min{|
|}≥min{| ![]() |,|
|,| ![]() |}
|}
C.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≤|
|2}≤| ![]() |2+|
|2+| ![]() |2
|2
D.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≥|
|2}≥| ![]() |2
|2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在一次抽樣調(diào)查中測得樣本的6組數(shù)據(jù),得到一個變量![]() 關(guān)于
關(guān)于![]() 的回歸方程模型,其對應的數(shù)值如下表:
的回歸方程模型,其對應的數(shù)值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)請用相關(guān)系數(shù)![]() 加以說明
加以說明![]() 與
與![]() 之間存在線性相關(guān)關(guān)系(當
之間存在線性相關(guān)關(guān)系(當![]() 時,說明
時,說明![]() 與
與![]() 之間具有線性相關(guān)關(guān)系);
之間具有線性相關(guān)關(guān)系);
(2)根據(jù)(1)的判斷結(jié)果,建立![]() 關(guān)于
關(guān)于![]() 的回歸方程并預測當
的回歸方程并預測當![]() 時,對應的
時,對應的![]() 值為多少(
值為多少(![]() 精確到
精確到![]() ).
).
附參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
 ,
,![]() ,相關(guān)系數(shù)
,相關(guān)系數(shù)![]() 公式為:
公式為: .
.
參考數(shù)據(jù):
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】5名師生站成一排照相留念,其中教師1人,男生2人,女生2人.
(1)求兩名女生相鄰而站的概率;
(2)求教師不站中間且女生不站兩端的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 是
是![]() 展開式中所有無理項的二項式系數(shù)和,數(shù)列
展開式中所有無理項的二項式系數(shù)和,數(shù)列![]() 是各項都大于1的數(shù)組成的數(shù)列,試用數(shù)學歸納法證明:
是各項都大于1的數(shù)組成的數(shù)列,試用數(shù)學歸納法證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,函數(shù)
,函數(shù)![]() .
.
![]() 若
若![]() 的最大值為0,記
的最大值為0,記![]() ,求
,求![]() 的值;
的值;
![]() 當
當![]() 時,記不等式
時,記不等式![]() 的解集為M,求函數(shù)
的解集為M,求函數(shù)![]() ,
,![]() 的值域
的值域![]() 是自然對數(shù)的底數(shù)
是自然對數(shù)的底數(shù)![]() ;
;
![]() 當
當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的零點個數(shù).
的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設常數(shù)a使方程sinx+ ![]() cosx=a在閉區(qū)間[0,2π]上恰有三個解x1 , x2 , x3 , 則x1+x2+x3= .
cosx=a在閉區(qū)間[0,2π]上恰有三個解x1 , x2 , x3 , 則x1+x2+x3= .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)若函數(shù)![]() 在
在![]() 時有極值,求
時有極值,求![]() 表達式;
表達式;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,求實數(shù)
上單調(diào)遞增,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com