
【題目】設離心率為 ![]() 的橢圓
的橢圓![]() 的左、右焦點為
的左、右焦點為![]() , 點P是E上一點,
, 點P是E上一點, ![]() ,
, ![]() 內切圓的半徑為
內切圓的半徑為 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的兩頂點C、D在直線![]() 上,A、B在橢圓E上,若矩形ABCD的周長為
上,A、B在橢圓E上,若矩形ABCD的周長為 ![]() , 求直線AB的方程.
, 求直線AB的方程.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() .過原點
.過原點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 上的點,若
上的點,若![]() ,
, ![]() ,且
,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2) 設橢圓在點![]() 處的切線記為直線
處的切線記為直線![]() ,點
,點![]() 在
在![]() 上的射影分別為
上的射影分別為![]() ,過
,過![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,試問
,試問![]() 是否為定值?若是,求出該定值;若不是,請說明理由.
是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不等式組 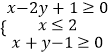 表示的平面區域為D,則
表示的平面區域為D,則
(1)z=x2+y2的最小值為 .
(2)若函數y=|2x﹣1|+m的圖象上存在區域D上的點,則實數m的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的100位顧客的相關數據,如下表所示.
一次購物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顧客數(人) | x | 30 | 25 | y | 10 |
結算時間(分鐘/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知這100位顧客中一次購物量超過8件的顧客占55%.
(Ⅰ)確定x,y的值,并求顧客一次購物的結算時間X的分布列與數學期望;
(Ⅱ)若某顧客到達收銀臺時前面恰有2位顧客需結算,且各顧客的結算相互獨立,求該顧客結算前的等候時間不超過2.5分鐘的概率.
(注:將頻率視為概率)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=a,an+1= ![]() (n∈N*).
(n∈N*).
(1)求a2 , a3 , a4;
(2)猜測數列{an}的通項公式,并用數學歸納法證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對一批產品的長度(單位:mm)進行抽樣檢測,下圖為檢測結果的頻率分布直方圖.根據標準,產品長度在區間[20,25)上的為一等品,在區間[15,20)和區間[25,30)上的為二等品,在區間[10,15)和[30,35)上的為三等品.用頻率估計概率,現從該批產品中隨機抽取一件,則其為二等品的概率為( ) 
A.0.09
B.0.20
C.0.25
D.0.45
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域是D,若存在常數m、M,使得m≤f(x)≤M對任意x∈D成立,則稱函數f(x)是D上的有界函數,其中m稱為函數f(x)的下界,M稱為函數f(x)的上界;特別地,若“=”成立,則m稱為函數f(x)的下確界,M稱為函數f(x)的上確界. (Ⅰ)判斷 ![]() 是否是有界函數?說明理由;
是否是有界函數?說明理由;
(Ⅱ)若函數f(x)=1+a2x+4x(x∈(﹣∞,0))是以﹣3為下界、3為上界的有界函數,求實數a的取值范圍;
(Ⅲ)若函數 ![]() ,T(a)是f(x)的上確界,求T(a)的取值范圍.
,T(a)是f(x)的上確界,求T(a)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知對任意平面向量 ![]() =(x,y),把
=(x,y),把 ![]() 繞其起點沿逆時針方向旋轉θ角得到的向量
繞其起點沿逆時針方向旋轉θ角得到的向量 ![]() =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把點B繞點A逆時針方向旋轉θ得到點P.
=(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把點B繞點A逆時針方向旋轉θ得到點P.
(1)已知平面內點A(2,3),點B(2+2 ![]() ,1).把點B繞點A逆時針方向旋轉
,1).把點B繞點A逆時針方向旋轉 ![]() 角得到點P,求點P的坐標.
角得到點P,求點P的坐標.
(2)設平面內曲線C上的每一點繞坐標原點沿順時針方向旋轉 ![]() 后得到的點的軌跡方程是曲線y=
后得到的點的軌跡方程是曲線y= ![]() ,求原來曲線C的方程.
,求原來曲線C的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com