
【題目】如圖是某直三棱柱(側棱與底面垂直的三棱柱)被削去上底后的直觀圖與三視圖中的側視圖、俯視圖,在直觀圖中, ![]() 是
是![]() 的中點,側視圖是直角梯形,俯視圖是等腰直角三角形,有關數據如圖所示.
的中點,側視圖是直角梯形,俯視圖是等腰直角三角形,有關數據如圖所示.
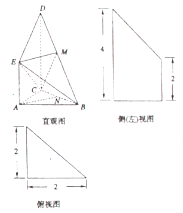
(1)求出該幾何體的體積;
(2)若![]() 是
是![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
【答案】(1) ![]() ;(2) 見解析.
;(2) 見解析.
【解析】試題分析:(1)先由面面垂直的性質定理證明![]() ,再由面面垂直的判定定理證明
,再由面面垂直的判定定理證明![]() 證明平面
證明平面![]() ,從而由棱錐的體積公式可得結果;(2)連接
,從而由棱錐的體積公式可得結果;(2)連接![]() ,由中位線定理得
,由中位線定理得![]() ,由平行四邊形可得
,由平行四邊形可得![]() ,進而可得結果.
,進而可得結果.
試題解析:(1)由題意可知:四棱錐![]() 中,
中,
平面![]() 平面
平面![]() ,
, ![]()
平面![]() 平面
平面![]()
所以, ![]() 平面
平面![]()
又![]() ,
, ![]() ,
,
則四棱錐![]() 的體積為:
的體積為: ![]()
(2)連接![]() ,則
,則![]() ,
, ![]()
又![]() ,所以四邊形
,所以四邊形![]() 為平心四邊形,
為平心四邊形, ![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以, ![]() 平面
平面![]()
【方法點晴】本題主要考查線面平行的判定定理、利用等積變換求三棱錐體積,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質,即兩平面平行,在其中一平面內的直線平行于另一平面. 本題(1)是就是利用方法①證明的.


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】上周某校高三年級學生參加了數學測試,年部組織任課教師對這次考試進行成績分析.現從中隨機選取了40名學生的成績作為樣本,已知這40名學生的成績全部在40分至100分之間(滿分100分,成績不低于40分),現將成績按如下方式分成6組:第一組![]() ;第二組
;第二組![]() ;……;第六組
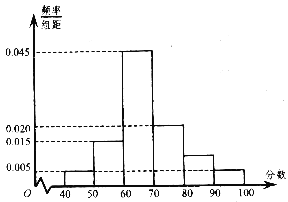
;……;第六組![]() ,并據此繪制了如圖所示的頻率分布直方圖.
,并據此繪制了如圖所示的頻率分布直方圖.
(Ⅰ)估計這次月考數學成績的平均分和眾數;
(Ⅱ)從成績大于等于80分的學生中隨機選2名,求至少有1名學生的成績在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位實行休年假制度三年以來,50名職工休年假的次數進行的調查統計結果如下表所示:
休假次數 | 0 | 1 | 2 | 3 |
人數 | 5 | 10 | 20 | 15 |
根據表中信息解答以下問題:
(1)從該單位任選兩名職工,求這兩人休年假次數之和為4的概率;
(2)從該單位任選兩名職工,用![]() 表示這兩人休年假次數之差的絕對值,求隨機變量
表示這兩人休年假次數之差的絕對值,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() 是橢圓的焦點,直線
是橢圓的焦點,直線![]() 的斜率為
的斜率為![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩個班級某次考試的數學成績(單位:分),從甲、乙兩個班級中分別隨機抽取5名學生的成績作樣本,如圖是樣本的莖葉圖.規定:成績不低于120分時為優秀成績.

(1)從甲班的樣本中有放回的隨機抽取 2 個數據,求其中只有一個優秀成績的概率;
(2)從甲、乙兩個班級的樣本中分別抽取2名同學的成績,記獲優秀成績的人數為![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了紀念“中國紅軍長征90周年”,增強學生對“長征精神”的深刻理解,在全校組織了一次有關“長征”的知識競賽,經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得20分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
, ![]() ,
, ![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(1)求![]() 的分布列和均值;
的分布列和均值;
(2)求甲、乙兩隊總得分之和等于40分且甲隊獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在心理學研究中,常采用對比試驗的方法評價不同心理暗示對人的影響,具體方法如下:將參加試驗的志愿者隨機分成兩組,一組接受甲種心理暗示,另一組接受乙種心理暗示,通過對比這兩組志愿者接受心理暗示后的結果來評價兩種心理暗示的作用,現有5名男志愿![]() 和3名女志愿者
和3名女志愿者![]() ,從中隨機抽取4人接受甲種心理暗示,另4人接受乙種心理暗示.
,從中隨機抽取4人接受甲種心理暗示,另4人接受乙種心理暗示.
(1)求接受甲種心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的頻率.
的頻率.
(2)用![]() 表示接受乙種心理暗示的女志愿者人數,求
表示接受乙種心理暗示的女志愿者人數,求![]() 的分布列與數學期望
的分布列與數學期望![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)若曲線![]() 在點
在點![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在區間
在區間![]() 上存在極值點,判斷該極值點是極大值點還是極小值點,并求
上存在極值點,判斷該極值點是極大值點還是極小值點,并求![]() 的取值范圍;
的取值范圍;
(3)若當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了降低能源消耗,某冷庫內部要建造可供使用20年的隔熱層,每厘米厚的隔熱層建造成本為4萬元,又知該冷庫每年的能源消耗費用![]() (單位:萬元)與隔熱層厚度
(單位:萬元)與隔熱層厚度![]() (單位:
(單位: ![]() )滿足關系
)滿足關系![]() ,若不建隔熱層,每年能源消耗為8萬元.設
,若不建隔熱層,每年能源消耗為8萬元.設![]() 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求![]() 的值及
的值及![]() 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用![]() 達到最小?并求最小值.
達到最小?并求最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com