
函數 是定義在
是定義在 上的偶函數,且對任意的
上的偶函數,且對任意的
 ,都有
,都有 .當
.當 時,
時, .若直線
.若直線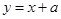 與函數
與函數 的圖象有兩個不同的公共點,則實數
的圖象有兩個不同的公共點,則實數 的值為( )
的值為( )
A.   | B.   |
C. 或 或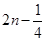  | D. 或 或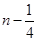  |
C
解析試題分析:解:因為函數f(x)是定義在R上的偶函數,設x∈[-1,0],則-x∈[0,1],于是f(x)=(-x)2=x2.
設x∈[1,2],則(x-2)∈[-1,0].于是,f(x)=f(x-2)=(x-2)2.
①當a=0時,聯立y="x," y=x2,解得x=0,y=0,或x=y=1,即當a=0時,即直線y=x+a與函數y=f(x)的圖象有兩個不同的公共點.
②當-2<a<0時,只有當直線y=x+a與函數f(x)=x2在區間[0,1)上相切,且與函數f(x)=(x-2)2在x∈[1,2)上僅有一個交點時才滿足條件.由f′(x)=2x=1,解得x= ∴y=(
∴y=( )2=
)2=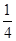 ,故其切點為(
,故其切點為( ,
,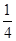 )
)
),∴a=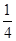 -
- =-
=-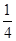 由y=x-
由y=x-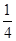 , y=(x-2)2(1≤x<2)解之得x=
, y=(x-2)2(1≤x<2)解之得x=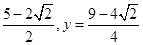 綜上①②可知:直線y=x+a與函數y=f(x)在區間[0,2)上的圖象有兩個不同的公共點時的a的值為0或-
綜上①②可知:直線y=x+a與函數y=f(x)在區間[0,2)上的圖象有兩個不同的公共點時的a的值為0或-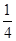 又函數f(x)是定義在R上的偶函數,且對任意的x∈R,都有f(x+2)=f(x),實數a的值為
又函數f(x)是定義在R上的偶函數,且對任意的x∈R,都有f(x+2)=f(x),實數a的值為 或
或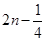 ,(n∈Z).故應選C.
,(n∈Z).故應選C.
考點:函數的奇偶性、周期性
點評:此題考查了函數的奇偶性、周期性及導數的應用,用到了數形結合的思想方法


 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com