
【題目】在正方體![]() 中,E是棱
中,E是棱![]() 的中點(diǎn),F是側(cè)面
的中點(diǎn),F是側(cè)面![]() 內(nèi)的動(dòng)點(diǎn),且
內(nèi)的動(dòng)點(diǎn),且![]() 與平面
與平面![]() 的垂線垂直,如圖所示,下列說法不正確的是( )
的垂線垂直,如圖所示,下列說法不正確的是( )
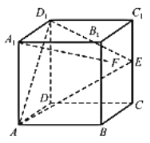
A.點(diǎn)F的軌跡是一條線段B.![]() 與BE是異面直線
與BE是異面直線
C.![]() 與
與![]() 不可能平行D.三棱錐
不可能平行D.三棱錐![]() 的體積為定值
的體積為定值
【答案】C
【解析】
分別根據(jù)線面平行的性質(zhì)定理以及異面直線的定義,體積公式分別進(jìn)行判斷.
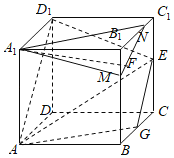
對于![]() ,設(shè)平面
,設(shè)平面![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,則
,則![]() 為
為![]() 的中點(diǎn)
的中點(diǎn)
分別取![]() 、
、![]() 的中點(diǎn)
的中點(diǎn)![]() 、
、![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .同理可得
.同理可得![]() 平面
平面![]() ,
,
![]() 、
、![]() 是平面
是平面![]() 內(nèi)的相交直線
內(nèi)的相交直線
![]() 平面
平面![]() 平面
平面![]() ,由此結(jié)合
,由此結(jié)合![]() 平面
平面![]() ,可得直線
,可得直線![]() 平面
平面![]() ,
,
即點(diǎn)![]() 是線段
是線段![]() 上上的動(dòng)點(diǎn).
上上的動(dòng)點(diǎn).![]() 正確.
正確.
對于![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,![]() 和平面
和平面![]() 相交,
相交,
![]() 與
與![]() 是異面直線,
是異面直線,![]() 正確.
正確.
對于![]() ,由
,由![]() 知,平面
知,平面![]() 平面
平面![]() ,
,
![]() 與
與![]() 不可能平行,
不可能平行,![]() 錯(cuò)誤.
錯(cuò)誤.
對于![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,則
,則![]() 到平面
到平面![]() 的距離是定值,三棱錐
的距離是定值,三棱錐![]() 的體積為定值,所以
的體積為定值,所以![]() 正確;
正確;
故選:![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在
在![]() 上是增函數(shù),求實(shí)數(shù)
上是增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若函數(shù)![]() 在
在![]() 上的最小值為3,求實(shí)數(shù)
上的最小值為3,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(2)設(shè)直線![]() 是曲線
是曲線![]() 的切線,若
的切線,若![]() 的斜率存在最小值-2,求
的斜率存在最小值-2,求![]() 的值,并求取得最小斜率時(shí)切線
的值,并求取得最小斜率時(shí)切線![]() 的方程.
的方程.
(3)已知![]() 分別在
分別在![]() ,
,![]() 處取得極值,求證:
處取得極值,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在R上的偶函數(shù)f(x)滿足f(x+2)=f(x),當(dāng)x∈[﹣3,﹣2]時(shí),f(x)=﹣x﹣2,則( )
A.![]() B.f(sin3)<f(cos3)
B.f(sin3)<f(cos3)
C.![]() D.f(2020)>f(2019)
D.f(2020)>f(2019)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)![]() ax﹣lnx(a∈R).
ax﹣lnx(a∈R).
(1)若a=2時(shí),求函數(shù)f(x)的單調(diào)區(qū)間;
(2)設(shè)g(x)=f(x)![]() 1,若函數(shù)g(x)在
1,若函數(shù)g(x)在![]() 上有兩個(gè)零點(diǎn),求實(shí)數(shù)a的取值范圍.
上有兩個(gè)零點(diǎn),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若方程![]() 所表示的曲線為C,給出下列四個(gè)命題:
所表示的曲線為C,給出下列四個(gè)命題:
①若C為橢圓,則1<t<4且t≠![]() ;
;
②若C為雙曲線,則t>4或t<1;
③曲線C不可能是圓;
④若C表示橢圓,且長軸在x軸上,則1<t<![]() .
.
其中正確的命題是________(把所有正確命題的序號都填在橫線上).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() 。
。
(Ⅰ)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求滿足上述條件的最大整數(shù)M;
(Ⅱ)如果對于任意的![]() 都有f(s)≥g(t)成立,求實(shí)數(shù)a的取值范圍.
都有f(s)≥g(t)成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
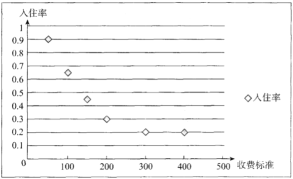
【題目】近年來,隨著互聯(lián)網(wǎng)技術(shù)的快速發(fā)展,共享經(jīng)濟(jì)覆蓋的范圍迅速擴(kuò)張,繼共享單車、共享汽車之后,共享房屋以“民宿”、“農(nóng)家樂”等形式開始在很多平臺上線.某創(chuàng)業(yè)者計(jì)劃在某景區(qū)附近租賃一套農(nóng)房發(fā)展成特色“農(nóng)家樂”,為了確定未來發(fā)展方向,此創(chuàng)業(yè)者對該景區(qū)附近六家“農(nóng)家樂”跟蹤調(diào)查了![]() 天.得到的統(tǒng)計(jì)數(shù)據(jù)如下表,
天.得到的統(tǒng)計(jì)數(shù)據(jù)如下表,![]() 為收費(fèi)標(biāo)準(zhǔn)(單位:元/日),
為收費(fèi)標(biāo)準(zhǔn)(單位:元/日),![]() 為入住天數(shù)(單位:),以頻率作為各自的“入住率”,收費(fèi)標(biāo)準(zhǔn)
為入住天數(shù)(單位:),以頻率作為各自的“入住率”,收費(fèi)標(biāo)準(zhǔn)![]() 與“入住率”
與“入住率”![]() 的散點(diǎn)圖如圖
的散點(diǎn)圖如圖
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若從以上六家“農(nóng)家樂”中隨機(jī)抽取兩家深入調(diào)查,記![]() 為“入住率”超過
為“入住率”超過![]() 的農(nóng)家樂的個(gè)數(shù),求
的農(nóng)家樂的個(gè)數(shù),求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散點(diǎn)圖判斷
,由散點(diǎn)圖判斷![]() 與
與![]() 哪個(gè)更合適于此模型(給出判斷即可,不必說明理由)?并根據(jù)你的判斷結(jié)果求回歸方程.(
哪個(gè)更合適于此模型(給出判斷即可,不必說明理由)?并根據(jù)你的判斷結(jié)果求回歸方程.(![]() 結(jié)果保留一位小數(shù))
結(jié)果保留一位小數(shù))
(3)若一年按![]() 天計(jì)算,試估計(jì)收費(fèi)標(biāo)準(zhǔn)為多少時(shí),年銷售額
天計(jì)算,試估計(jì)收費(fèi)標(biāo)準(zhǔn)為多少時(shí),年銷售額![]()
![]() 入住率
入住率![]() 收費(fèi)標(biāo)準(zhǔn)
收費(fèi)標(biāo)準(zhǔn)![]() )
)
參考數(shù)據(jù):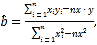
![]()
![]()
![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com