
(I)求橢圓C2的標準方程;
(II)設AB是過橢圓C,中心的任意弦,l是線段AB的垂直平分線,M是l上異于橢圓中心的點.
(1) 若|MO|=![]() |OA|(O為坐標原點),當點A在橢圓C2上運動時,求點M的軌跡方程;
|OA|(O為坐標原點),當點A在橢圓C2上運動時,求點M的軌跡方程;
(2)若M是l與橢圓C2的交點,求△AMB的面積的最小值。
解:(I)由題意得 由a>b>0,
由a>b>0,
解得 a2=5, b2=4.
因此所求橢圓的標準方程為 ![]()
![]() =1.
=1.
(II)(1)假設AB所在的直線斜率存在且不為零,設AB所在直線方程為y=kx(k≠0),
A(xA,yA).
解方程組 得
得
![]()
![]()
所以 |OA|2=![]()
設M(x,y),由題意知|MO|=λ|OA|(λ![]()
所以|MO|2=λ2|OA|2,即![]() ,
,
因為l是AB的垂直平分線,
所以 直線l的方程為y=-![]() ,
,
即k=-![]() ,
,
因此 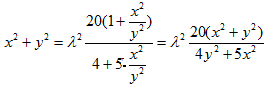
又x2+y2![]() ,
,
故 ![]() .
.
又 當k=0或不存時,上式仍然成立.
綜上所述,M的軌跡方程為![]() (λ
(λ![]() 0),
0),
(2) 當k存在且k![]() 0時,由(1)得
0時,由(1)得
![]() ,
,
由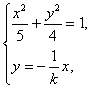 解得
解得
![]()
所以|OA|2=![]() ,
,
![]()
![]()
解法一:由于 ![]()
=![]()
=![]()
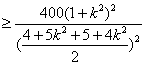
=![]()
=(![]() )2,
)2,
當且僅當4+5k2=5+4k2時等號成立,即k=![]() 1時等號成立,此時△AMB面積的最小值是S△AMB=
1時等號成立,此時△AMB面積的最小值是S△AMB=![]() .當
.當![]()
當k不存在時,![]()
綜上所述,![]() 的面積的最小值為
的面積的最小值為![]()
解法二:因為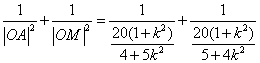
![]()
又 ![]()
當且僅當![]() 時等號成立,即
時等號成立,即![]() 時等號成立,此時
時等號成立,此時![]() 面積的最小值是
面積的最小值是![]()
當k=0,![]()
當k不存在時,![]()
綜上所述,![]() 的面積的最小值為
的面積的最小值為![]()


科目:高中數學 來源: 題型:
| |x| |
| a |
| |y| |
| b |
| 5 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源:山東 題型:解答題
| |x| |
| a |
| |y| |
| b |
| 5 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省德州市高三(上)校際聯考數學試卷(理科)(解析版) 題型:填空題
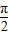 在第一象限所圍成的封閉圖形的面積為 .
在第一象限所圍成的封閉圖形的面積為 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com