
【題目】已知三棱柱![]() 的底面是正三角形,側面
的底面是正三角形,側面![]() 為菱形,且
為菱形,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.
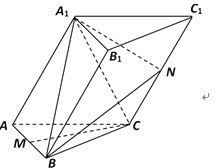
(I)求證:![]() ∥平面
∥平面![]() ;
;
(II)求證:![]() ;
;
(III)求BA1與平面![]() 所成角的大小.
所成角的大小.
【答案】(1)見解析.
(2)見解析.
(3)![]() .
.
【解析】分析:(Ⅰ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() .可證明四邊形
.可證明四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ∥
∥![]() ,由線面平行的判定定理可得結果;(II)取
,由線面平行的判定定理可得結果;(II)取![]() 的中點
的中點![]() ,連結
,連結![]() ,
,![]() ,由面面垂直的性質可得
,由面面垂直的性質可得![]() 平面
平面![]() , 所以
, 所以![]() ,由菱形的性質結合
,由菱形的性質結合![]() ∥
∥![]() , 可得
, 可得![]() ,從而得
,從而得![]() 平面
平面![]() ,進而可得結果;(III)連結A1O,由(Ⅱ)知
,進而可得結果;(III)連結A1O,由(Ⅱ)知![]() 平面
平面![]() 所以
所以![]() 為BA1與平面
為BA1與平面![]() 所成的角 ,在直角三角形
所成的角 ,在直角三角形![]() 中,
中,![]() ,從而可得結果.
,從而可得結果.
詳解:

證明:(Ⅰ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() .
.
因為![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,
所以![]() ∥
∥![]() ,
,![]()
又因為![]() ∥
∥![]()
所以![]() ∥
∥![]() 且
且![]()
所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ∥
∥![]() .
.
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(Ⅱ)取![]() 的中點
的中點![]() ,連結
,連結![]() ,
,![]() .
.
由題意知![]()
![]() ,
,
又因為平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() 所以
所以![]()
因為四邊形![]() 為菱形,所以
為菱形,所以![]()
又因為![]() ∥
∥![]() , 所以
, 所以![]()
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
所以![]() .
.
(III)連結A1O,由(Ⅱ)知![]() 平面
平面![]()
所以![]() 為BA1與平面
為BA1與平面![]() 所成的角
所成的角
在直角三角形![]() 中,
中,![]()
所以![]() ,即BA1與平面
,即BA1與平面![]() 所成的角為
所成的角為![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,已知
,已知![]() ,其中
,其中![]() 為原點,
為原點,![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() ,求直線的
,求直線的![]() 斜率的取值范圍.
斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水仙花經營部每天的房租、水電、人工等固定成本為1000元,每盆水仙花的進價是10元,銷售單價![]() (元) (
(元) (![]() )與日均銷售量
)與日均銷售量![]() (盆)的關系如下表,并保證經營部每天盈利.
(盆)的關系如下表,并保證經營部每天盈利.
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
(Ⅰ) 在所給的坐標圖紙中,根據表中提供的數據,描出實數對![]() 的對應點,并確定
的對應點,并確定![]() 與
與![]() 的函數關系式;
的函數關系式;
(Ⅱ)求出![]() 的值,并解釋其實際意義;
的值,并解釋其實際意義;
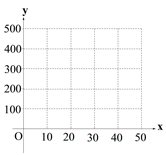
(Ⅲ)請寫出該經營部的日銷售利潤![]() 的表達式,并回答該經營部怎樣定價才能獲最大日銷售利潤?
的表達式,并回答該經營部怎樣定價才能獲最大日銷售利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高級中學今年高一年級招收“國際班”學生![]() 人,學校為這些學生開辟了直升海外一流大學的綠色通道,為了逐步提高這些學生與國際教育接軌的能力,將這
人,學校為這些學生開辟了直升海外一流大學的綠色通道,為了逐步提高這些學生與國際教育接軌的能力,將這![]() 人分為三個批次參加國際教育研修培訓,在這三個批次的學生中男、女學生人數如下表:
人分為三個批次參加國際教育研修培訓,在這三個批次的學生中男、女學生人數如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名,抽到第一批次、第二批次中女學生的概率分別是
名,抽到第一批次、第二批次中女學生的概率分別是![]() .
.
(1)求![]() 的值;
的值;
(2)為了檢驗研修的效果,現從三個批次中按分層抽樣的方法抽取![]() 名同學問卷調查,則三個批次被選取的人數分別是多少?
名同學問卷調查,則三個批次被選取的人數分別是多少?
(3)若從第(2)小問選取的學生中隨機選出兩名學生進行訪談,求“參加訪談的兩名同學至少有一個人來自第一批次”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x>0,由不等式x+ ![]() ≥2
≥2 ![]() =2,x+
=2,x+ ![]() =
= ![]() ≥3
≥3 ![]() =3,…,可以推出結論:x+
=3,…,可以推出結論:x+ ![]() ≥n+1(n∈N*),則a=( )
≥n+1(n∈N*),則a=( )
A.2n
B.3n
C.n2
D.nn
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足:
滿足:![]() ,
,![]() ,且
,且![]() (n=1,2,...).記
(n=1,2,...).記
集合![]() .
.
(1)(Ⅰ)若![]() ,寫出集合M的所有元素;
,寫出集合M的所有元素;
(2)(Ⅱ)若集合M存在一個元素是3的倍數,證明:M的所有元素都是3的倍數;
(3)(Ⅲ)求集合M的元素個數的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ,且
,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)將函數 ![]() 的圖像向右平移
的圖像向右平移 ![]() 個單位長度得到函數
個單位長度得到函數 ![]() 的圖像,若函數
的圖像,若函數 ![]() 在
在 ![]() 上有零點,求
上有零點,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖的程序框圖表示的算法中,輸入三個實數a,b,c,要求輸出的x是這三個數中最大的數,那么在空白的判斷框中,應該填入( ) 
A.x>c
B.c>x
C.c>b
D.c>a
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi , yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為 ![]() =0.85x﹣85.71,則下列結論中不正確的是( )
=0.85x﹣85.71,則下列結論中不正確的是( )
A.y與x具有正的線性相關關系
B.回歸直線過樣本點的中心( ![]() ,
, ![]() )
)
C.若該大學某女生身高增加1cm,則其體重約增加0.85kg
D.若該大學某女生身高為170cm,則可斷定其體重必為58.79kg
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com