Question

（06年天津卷理）（14分）

如圖，以橢圓的中心O為圓心，分別以和為半徑作大圓和小圓。過橢圓右焦點作垂直于軸的直線交大圓于第一象限內的點A。連結OA交小圓于點B。設直線BF是小圓的切線。

  

（I）證明并求直線BF與同的交點M的坐標；

（II）設直線BF交橢圓P、Q兩點，證明

Answer 1

解析：（I）證明：由題設條件知，故

                     即

       因此，　　　　①

       在中，

       于是，直線OA的斜率設直線BF的斜率為則

                    

       這時，直線BF的方程為令則

       所以直線BF與軸的交點為

 

（II）證明：由（I），得直線的方程為且

                     　　　　　　②

       由已知，設、則它們的坐標滿足方程組

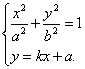                     　　　　　　　　③

       由方程組③消去并整理得

                     　　　④

       由式①、②和④，

                    

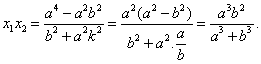
       由方程組③消去并整理得

                     　　⑤

       由式②和⑤，

                    

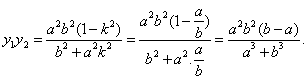
       綜上，得到

                    

       注意到得

                    

　　　　　　　　　

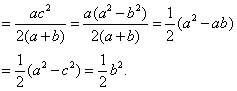
【高考考點】橢圓的標準方程和幾何性質　直線方程　平面向量　曲線和方程的關系

【易錯點】：不能找出隱含條件結合完成第一問證明，第二問到的計算及向結論的化簡過程

【備考提示】：掌握橢圓的幾何性質，善于找出已知中的隱含條件是解決此題的關鍵