
【題目】某市需對某環城快速車道進行限速,為了調研該道路車速情況,于某個時段隨機對 ![]() 輛車的速度進行取樣,測量的車速制成如下條形圖:
輛車的速度進行取樣,測量的車速制成如下條形圖:
經計算:樣本的平均值 ![]() ,標準差
,標準差 ![]() ,以頻率值作為概率的估計值.已知車速過慢與過快都被認為是需矯正速度,現規定車速小于
,以頻率值作為概率的估計值.已知車速過慢與過快都被認為是需矯正速度,現規定車速小于 ![]() 或車速大于
或車速大于 ![]() 是需矯正速度.
是需矯正速度.
(1)從該快速車道上所有車輛中任取 ![]() 個,求該車輛是需矯正速度的概率;
個,求該車輛是需矯正速度的概率;
(2) 從樣本中任取
從樣本中任取 ![]() 個車輛,求這
個車輛,求這 ![]() 個車輛均是需矯正速度的概率
個車輛均是需矯正速度的概率
(3)從該快速車道上所有車輛中任取 ![]() 個,記其中是需矯正速度的個數為
個,記其中是需矯正速度的個數為 ![]() ,求
,求 ![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】
(1)解:記事件 ![]() 為“從該快速車道上所有車輛中任取
為“從該快速車道上所有車輛中任取 ![]() 個,該車輛是需矯正速度”,
個,該車輛是需矯正速度”,
因為 ![]() ,
,
由樣本條形圖可知,所求的概率為P(A)=![]()
(2)解:記事件 ![]() 為“從樣本中任取
為“從樣本中任取 ![]() 個車輛,這
個車輛,這 ![]() 個車輛均是需矯正速度”
個車輛均是需矯正速度”
由題設可知樣本容量為 ![]() ,又需矯正速度個數為
,又需矯正速度個數為 ![]() 個,故所求概率為
個,故所求概率為 ![]()
(3)解:需矯正速度的個數 ![]() 服從二項分布,即
服從二項分布,即 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
![]() ,
,
因此 ![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
由 ![]() ,知數學期望
,知數學期望 ![]()
【解析】(1)根據題意由已知可得出 μ 3 σ = 78.4 , μ + 2 σ = 89.4,觀察樣本條形圖由圖可知P(A)=![]() 求出其值即可。(2)利用已知由題設可知樣本容量為100,又需矯正速度個數為 5 個根據概率的定義求出比值。(3)按照二項分布的公式
求出其值即可。(2)利用已知由題設可知樣本容量為100,又需矯正速度個數為 5 個根據概率的定義求出比值。(3)按照二項分布的公式![]() 逐一代入數值計算出結果列表即可,再結合數學期望
逐一代入數值計算出結果列表即可,再結合數學期望![]() 的公式代入數值求出即可。
的公式代入數值求出即可。
【考點精析】通過靈活運用用樣本的頻率分布估計總體分布,掌握樣本數據的頻率分布表和頻率分布直方圖,是通過各小組數據在樣本容量中所占比例大小來表示數據的分布規律,它可以讓我們更清楚的看到整個樣本數據的頻率分布情況,并由此估計總體的分布情況即可以解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在如圖所示的多面體中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中點.
(1)求證:BD⊥EG;
(2)求平面DEG與平面DEF所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是函數 ![]() 圖象的一部分.為了得到這個函數的圖象,只要將y=sinx(x∈R)的圖象上所有的點( )
圖象的一部分.為了得到這個函數的圖象,只要將y=sinx(x∈R)的圖象上所有的點( )
A.向左平移 ![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 ![]() ,縱坐標不變
,縱坐標不變
B.向左平移 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
C.向左平移 ![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 ![]() ,縱坐標不變
,縱坐標不變
D.向左平移 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近期“共享單車”在全國多個城市持續升溫,某移動互聯網機構通過對使用者的調查得出,現在市場上常見的八個品牌的“共享單車”的滿意度指數如莖葉圖所示:
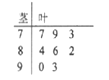
(Ⅰ)求出這組數據的平均數和中位數;
(Ⅱ)某用戶從滿意度指數超過80的品牌中隨機選擇兩個品牌使用,求所選兩個品牌的滿意度指數均超過85的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將圓 ![]() 為參數)上的每一點的橫坐標保持不變,縱坐標變為原來的
為參數)上的每一點的橫坐標保持不變,縱坐標變為原來的 ![]() 倍,得到曲線C.
倍,得到曲線C.
(1)求出C的普通方程;
(2)設直線l:x+2y﹣2=0與C的交點為P1 , P2 , 以坐標原點為極點,x軸正半軸為極軸建立極坐標系, 求過線段P1P2的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個小球從100米高處自由落下,每次著地后又跳回到原高度的一半再落下.執行下面的程序框圖,則輸出的S表示的是( ) 
A.小球第10次著地時向下的運動共經過的路程
B.小球第11次著地時向下的運動共經過的路程
C.小球第10次著地時一共經過的路程
D.小球第11次著地時一共經過的路程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com