Question

下列函數中，既是偶函數又在區間單調遞增的函數是（    ）

A．

B．

C．

D．

Answer 1

D

解析試題分析：根據函數奇偶性以及單調性的概念，那么可知
選項A中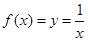，，定義域關于原點對稱，且有是奇函數。不符合題意。
而選項B中，由于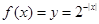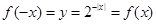，，因此是偶函數， 當時利用復合函數單調性的判定可知，當x>0時，外層函數遞增，內層函數遞減，則復合函數是遞減的。錯誤。
選項C中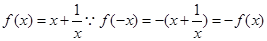，是奇函數， 不符合。
選項D，作為二次函數，開口向上，對稱軸為y軸，顯然是偶函數，同時也是定義域內增函數，因此成立。故選D.
考點：本試題考查了函數的奇偶性和函數單調性的概念。
點評：對于函數的奇偶性的判定，一般要抓住兩點：定義域是否關于原點對稱，同時解析式f(-x)與f(x)的和為零，還是差為零來得到判定，而單調性的問題，主要是熟悉常見的基本初等函數的單調性，結合性質來判定，屬于基礎題。