
【題目】在四棱錐![]() 中,平面
中,平面![]() 平面PCD,底面ABCD為梯形,
平面PCD,底面ABCD為梯形,![]() ,
,![]() ,M為PD的中點,過A,B,M的平面與PC交于N.
,M為PD的中點,過A,B,M的平面與PC交于N.![]() ,
,![]() ,
,![]() ,
,![]() .
.
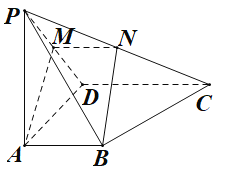
(1)求證:N為PC中點;
(2)求證:![]() 平面PCD;
平面PCD;
(3)T為PB中點,求二面角![]() 的大小.
的大小.
【答案】(1)證明見解析;(2)證明見解析;(3)45°
【解析】
(1)利用線面平行的性質可得![]() ,又由M為PD的中點,即可求證N為PC中點;
,又由M為PD的中點,即可求證N為PC中點;
(2)利用面面垂直的性質,可過點![]() 作
作![]() ,可證
,可證![]() ,再結合線面垂直的判定定理即可求證;
,再結合線面垂直的判定定理即可求證;
(3)采用建系法以![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸建立空間直角坐標系,利用向量法即可求出二面角
軸建立空間直角坐標系,利用向量法即可求出二面角![]() 的大小
的大小
(1)![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
由線面平行的性質可得,![]() ,
,
又![]() ,
,![]() ,
,
![]() M為PD的中點,
M為PD的中點,![]() 為PC的中點;
為PC的中點;
(2)過點![]() 作
作![]() 交
交![]() 與點
與點![]() ,
,
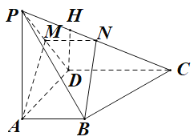
又![]() 平面
平面![]() 平面PCD,交線為
平面PCD,交線為![]() ,故
,故![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]()
![]() 平面PCD;
平面PCD;
(3)由(2)可知![]() 平面PCD,
平面PCD,![]() ,故以
,故以![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸建立空間直角坐標系,如圖:
軸建立空間直角坐標系,如圖:
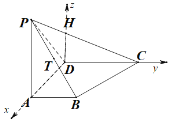
求得![]() ,
,
![]() 為
為![]() 的中點,故
的中點,故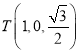 ,
,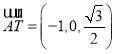 ,
,![]() ,
,
可設平面![]() 的法向量為
的法向量為![]() ,平面
,平面![]() 的法向量為
的法向量為![]() ,故有
,故有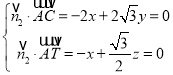 ,取
,取![]() 得
得![]() ,則
,則![]() ,故
,故
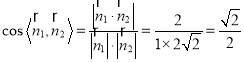 ,故二面角
,故二面角![]() 的大小為45°
的大小為45°


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:高中數學 來源: 題型:
【題目】數列![]() :
: ![]() 滿足:
滿足: ![]() ,
, ![]() 或1(
或1(![]() ).對任意
).對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且兩兩不相等.
且兩兩不相等.
(I)若![]() .寫出下列三個數列中所有符合題目條件的數列的序號;
.寫出下列三個數列中所有符合題目條件的數列的序號;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)記![]() .若
.若![]() ,證明:
,證明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均為正實數,且滿足a+b+c=m,求證:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟水平及個人消費能力的提升,我國居民對精神層面的追求愈加迫切,如圖是2007年到2017年我國城鎮居民教育、文化、服務人均消費支出同比增速的折線圖,圖中顯示2007年的同比增速為10%, 即2007年與2006年同時期比較2007年的人均消費支出費用是2006年的1.1倍.則下列表述中正確的是( )
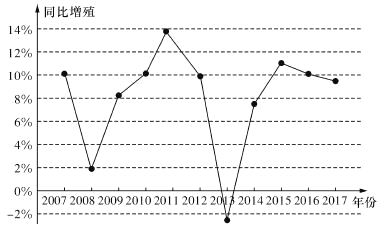
A.2007年到2017年,同比增速的中位數約為10%
B.2007年到2017年,同比增速的極差約為12%
C.2011年我國城鎮居民教育、文化、服務人均消費支出的費用最高
D.2007年到2017年,我國城鎮居民教育、文化、服務人均消費支出的費用逐年增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上一點,且
上一點,且![]() .三棱錐
.三棱錐![]() 的各個頂點都在球
的各個頂點都在球![]() 表面上,過點
表面上,過點![]() 作球
作球![]() 的截面,若所得截面圓的面積的最大值與最小值之差為
的截面,若所得截面圓的面積的最大值與最小值之差為![]() ,則球
,則球![]() 的表面積為( )
的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某同學在素質教育基地通過自己設計、選料、制作,打磨出了一個作品,作品由三根木棒![]() ,
,![]() ,
,![]() 組成,三根木棒有相同的端點
組成,三根木棒有相同的端點![]() (粗細忽略不計),且
(粗細忽略不計),且![]() 四點在同一平面內,
四點在同一平面內,![]()
![]() ,
,![]() ,木棒
,木棒![]() 可繞點O任意旋轉,設BC的中點為D.
可繞點O任意旋轉,設BC的中點為D.
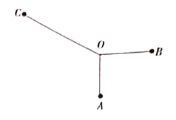
(1)當![]() 時,求OD的長;
時,求OD的長;
(2)當木棒OC繞點O任意旋轉時,求AD的長的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,且
,且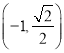 在橢圓E上.
在橢圓E上.
(1)求橢圓E的標準方程;
(2)已知垂直于x軸的直線![]() 交E于A、B兩點,垂直于y軸的直線
交E于A、B兩點,垂直于y軸的直線![]() 交E于C、D兩點,
交E于C、D兩點,![]() 與
與![]() 的交點為P,且
的交點為P,且![]() ,間:是否存在兩定點M,N,使得
,間:是否存在兩定點M,N,使得![]() 為定值?若存在,求出M,N的坐標,若不存在,請說明理由.
為定值?若存在,求出M,N的坐標,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com