
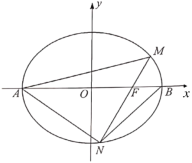
【題目】如圖,點(diǎn)![]() 分別為橢圓
分別為橢圓![]() 的左右頂點(diǎn)和右焦點(diǎn),過(guò)點(diǎn)
的左右頂點(diǎn)和右焦點(diǎn),過(guò)點(diǎn)![]() 的直線交橢圓
的直線交橢圓![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)若![]() ,點(diǎn)
,點(diǎn)![]() 與橢圓
與橢圓![]() 左準(zhǔn)線的距離為
左準(zhǔn)線的距離為![]() ,求橢圓
,求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 的斜率是直線
的斜率是直線![]() 斜率的
斜率的![]() 倍.
倍.
①求橢圓![]() 的離心率;
的離心率;
②若橢圓![]() 的焦距為
的焦距為![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() .(2)①
.(2)①![]() ;②
;②![]()
【解析】
由所給條件列出關(guān)于![]() 的式子,求出橢圓方程;(2)①方法一,首先利用點(diǎn)在橢圓上,求得
的式子,求出橢圓方程;(2)①方法一,首先利用點(diǎn)在橢圓上,求得![]() ,再利用直線
,再利用直線![]() 方程與橢圓方程聯(lián)立,求得
方程與橢圓方程聯(lián)立,求得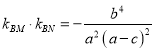 ,再利用
,再利用![]() 的關(guān)系,求得橢圓離心率;方法二,利用
的關(guān)系,求得橢圓離心率;方法二,利用![]() 的關(guān)系,分別設(shè)直線
的關(guān)系,分別設(shè)直線![]() 的方程為
的方程為![]() ,直線
,直線![]() 的方程為
的方程為![]() ,與橢圓方程聯(lián)立,解出點(diǎn)
,與橢圓方程聯(lián)立,解出點(diǎn)![]() 的坐標(biāo),利用點(diǎn)
的坐標(biāo),利用點(diǎn)![]() 三點(diǎn)共線,求得離心率.②首先求得橢圓方程,并表示
三點(diǎn)共線,求得離心率.②首先求得橢圓方程,并表示![]() 面積
面積![]() ,由①方法一,代入根與系數(shù)的關(guān)系,求
,由①方法一,代入根與系數(shù)的關(guān)系,求![]() 面積的最大值.
面積的最大值.
(1)∵![]() ,點(diǎn)
,點(diǎn)![]() 與橢圓
與橢圓![]() 左準(zhǔn)線的距離為
左準(zhǔn)線的距離為![]() ,
,
∴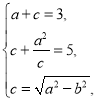 解得
解得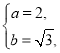
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)①法一:顯然![]() ,
,![]() ,
,![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
則∵點(diǎn)![]() 在橢圓
在橢圓![]() 上,∴
上,∴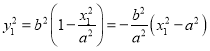 ,
,
∴![]() (i),
(i),
設(shè)直線![]() ,
,
與橢圓![]() 聯(lián)立方程組消去
聯(lián)立方程組消去![]() 得:
得:
![]() ,其兩根為
,其兩根為![]() ,
,
∴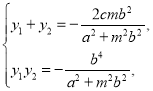 (*)
(*)
∴![]()
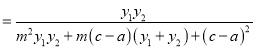 ,
,
將(*)代入上式化簡(jiǎn)得: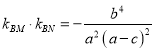 (ii)
(ii)
又![]() (iii)
(iii)
由(i)(ii)(iii)得: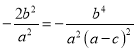 ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,∴
,∴![]() ,即橢圓
,即橢圓![]() 的離心率為
的離心率為![]() .
.
法二:顯然![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴設(shè)直線
,∴設(shè)直線![]() 的方程為
的方程為![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
由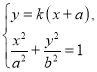 得
得![]() ,
,
注意到其一根為![]() ,∴另一根為
,∴另一根為![]() ,
,
∴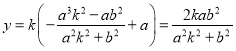 ,即
,即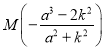 ,
,
同理由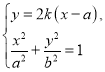 得
得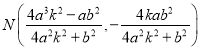 .
.
由![]() 三點(diǎn)共線得
三點(diǎn)共線得![]() ,
,
∴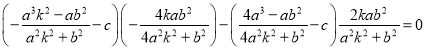 ,
,
化簡(jiǎn)得:![]() ,∴
,∴![]() ,
,
∴![]() ,即橢圓
,即橢圓![]() 的離心率為
的離心率為![]() .
.
②由①![]() ,又橢圓
,又橢圓![]() 的焦距為
的焦距為![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由①方法一得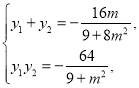
∴![]() 面積
面積![]()
![]() ,
,![]()
令![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
∵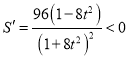 ,∴
,∴![]() 在
在![]() 為減函數(shù),
為減函數(shù),
∴![]() ,即
,即![]() 時(shí),
時(shí),![]() ,即
,即![]() 面積的最大值為
面積的最大值為![]() .
.


 優(yōu)質(zhì)課堂快樂(lè)成長(zhǎng)系列答案
優(yōu)質(zhì)課堂快樂(lè)成長(zhǎng)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)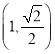 ,
,![]() ,
,![]() 是C的左、右焦點(diǎn),過(guò)
是C的左、右焦點(diǎn),過(guò)![]() 的直線l與C交于A,B兩點(diǎn),且
的直線l與C交于A,B兩點(diǎn),且![]() 的周長(zhǎng)為
的周長(zhǎng)為![]() .
.
(1)求C的方程;
(2)若![]() ,求l的方程.
,求l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】《九章算術(shù)》是我國(guó)古代數(shù)學(xué)名著,它在幾何學(xué)中的研究比西方早1000多年,在《九章算術(shù)》中,將底面為直角三角形,且側(cè)棱垂直于底面的三棱柱稱為塹堵(qian du);陽(yáng)馬指底面為矩形,一側(cè)棱垂直于底面的四棱錐,鱉膈(bie nao)指四個(gè)面均為直角三角形的四面體.如圖在塹堵![]() 中,
中,![]() ,
,![]() .給出下列四個(gè)結(jié)論:
.給出下列四個(gè)結(jié)論:
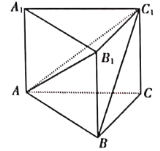
①四棱錐![]() 為陽(yáng)馬;
為陽(yáng)馬;
②直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ;
;
③當(dāng)![]() 時(shí),異面直線
時(shí),異面直線![]() 與
與![]() 所成的角的余弦值為
所成的角的余弦值為![]() ;
;
④當(dāng)三棱錐![]() 體積最大時(shí),四棱錐
體積最大時(shí),四棱錐![]() 的外接球的表面積為
的外接球的表面積為![]() .
.
其中,所有正確結(jié)論的序號(hào)是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩地相距300千米,汽車從甲地勻速行駛到乙地,速度不超過(guò)100千米/小時(shí),已知汽車每小時(shí)的運(yùn)輸成本(以元為單位)由可變部分和固定部分組成,可變部分與速度![]() (千米/小時(shí))的平方成正比,比例系數(shù)為
(千米/小時(shí))的平方成正比,比例系數(shù)為![]() (
(![]() ),固定部分為1000元.
),固定部分為1000元.
(1)把全程運(yùn)輸成本![]() (元)表示為速度
(元)表示為速度![]() (千米/小時(shí))的函數(shù),并指出這個(gè)函數(shù)的定義域;
(千米/小時(shí))的函數(shù),并指出這個(gè)函數(shù)的定義域;
(2)為了使全程運(yùn)輸成本最小,汽車應(yīng)以多大速度行駛?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為
中,以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為![]() ,曲線C的極坐標(biāo)方程為
,曲線C的極坐標(biāo)方程為![]() .
.
(Ⅰ)求直線l和曲線C的直角坐標(biāo)方程;
(Ⅱ)點(diǎn)M為曲線C上一點(diǎn),求M到直線l的最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在①![]() 是
是![]() 與
與![]() 的等差中項(xiàng);②
的等差中項(xiàng);②![]() 是
是![]() 與
與![]() 的等比中項(xiàng);③數(shù)列
的等比中項(xiàng);③數(shù)列![]() 的前5項(xiàng)和為65這三個(gè)條件中任選一個(gè),補(bǔ)充在橫線中,并解答下面的問(wèn)題.
的前5項(xiàng)和為65這三個(gè)條件中任選一個(gè),補(bǔ)充在橫線中,并解答下面的問(wèn)題.
已知![]() 是公差為2的等差數(shù)列,其前
是公差為2的等差數(shù)列,其前![]() 項(xiàng)和為
項(xiàng)和為![]() ,________________________.
,________________________.
(1)求![]() ;
;
(2)設(shè)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說(shuō)明理由.
的值;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:若一個(gè)函數(shù)存在極大值,且該極大值為負(fù)數(shù),則稱這個(gè)函數(shù)為“![]() 函數(shù)”.
函數(shù)”.
(1)判斷函數(shù)![]() 是否為“
是否為“![]() 函數(shù)”,并說(shuō)明理由;
函數(shù)”,并說(shuō)明理由;
(2)若函數(shù)![]() 是“
是“![]() 函數(shù)”,求實(shí)數(shù)
函數(shù)”,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,
,![]() ,
,![]() 、
、![]() ,求證:當(dāng)
,求證:當(dāng)![]() ,且
,且![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 是“
是“![]() 函數(shù)”.
函數(shù)”.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)證明:![]() 有且只有一個(gè)零點(diǎn).
有且只有一個(gè)零點(diǎn).
(2)當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求整數(shù)
恒成立,求整數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知四棱錐![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
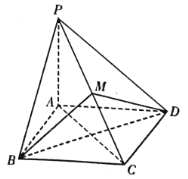
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com