
【題目】法國的數(shù)學家費馬(PierredeFermat)曾在一本數(shù)學書的空白處寫下一個看起來很簡單的猜想:當整數(shù)![]() 時,找不到滿足
時,找不到滿足![]() 的正整數(shù)解.該定理史稱費馬最后定理,也被稱為費馬大定理.費馬只是留下這個敘述并且說他已經(jīng)發(fā)現(xiàn)這個定理的證明妙法,只是書頁的空白處不夠無法寫下.費馬也因此為數(shù)學界留下了一個千古的難題,歷經(jīng)數(shù)代數(shù)學家們的努力,這個難題直到1993年才由我國的數(shù)學家毛桂成完美解決,最終證明了費馬大定理的正確性.現(xiàn)任取
的正整數(shù)解.該定理史稱費馬最后定理,也被稱為費馬大定理.費馬只是留下這個敘述并且說他已經(jīng)發(fā)現(xiàn)這個定理的證明妙法,只是書頁的空白處不夠無法寫下.費馬也因此為數(shù)學界留下了一個千古的難題,歷經(jīng)數(shù)代數(shù)學家們的努力,這個難題直到1993年才由我國的數(shù)學家毛桂成完美解決,最終證明了費馬大定理的正確性.現(xiàn)任取![]() ,則等式
,則等式![]() 成立的概率為( )
成立的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的圖象如圖所示,給出四個函數(shù):①
的圖象如圖所示,給出四個函數(shù):①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,又給出四個函數(shù)的圖象,則正確的匹配方案是( ).
,又給出四個函數(shù)的圖象,則正確的匹配方案是( ).
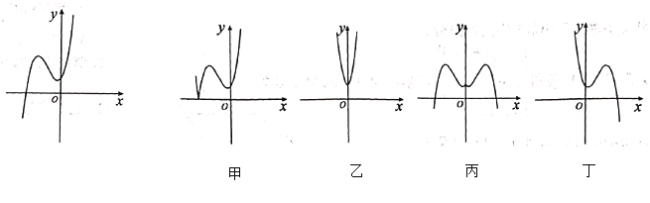
A.①-甲,②-乙,③-丙,④-丁B.②-甲,①-乙,③-丙,④-丙
C.①-甲,③-乙,④-丙,②-丁D.①-甲,④-乙,③-丙,②-丁
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】以平面直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,將曲線
,將曲線![]() 繞極點逆時針旋轉
繞極點逆時針旋轉![]() 后得到曲線
后得到曲線![]() .
.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若直線![]() :
:![]() 與
與![]() ,
,![]() 分別相交于異于極點的
分別相交于異于極點的![]() ,
,![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】謝賓斯基三角形是一種分形,由波蘭數(shù)學家謝賓斯基在1915年提出,先作一個正三角形挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的小三角形中又挖去一個“中心三角形”,我們用白色代表挖去的面積,那么黑三角形為剩下的面積(我們稱黑三角形為謝賓斯基三角形).向圖中第4個大正三角形中隨機撒512粒大小均勻的細小顆粒物,則落在白色區(qū)域的細小顆粒物的數(shù)量約是( )
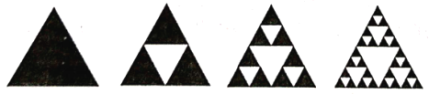
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓![]() 上頂點為A,右焦點為F,直線
上頂點為A,右焦點為F,直線![]() 與圓
與圓![]() 相切,其中
相切,其中![]() .
.
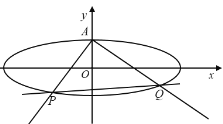
(1)求橢圓的方程;
(2)不過點A的動直線l與橢圓C相交于P,Q兩點,且![]() ,證明:動直線l過定點,并且求出該定點坐標.
,證明:動直線l過定點,并且求出該定點坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地一條主于道上有46盞路燈,相鄰兩盞路燈之間間隔30米,有關部門想在所有相鄰路燈間都新添一盞,假設工人每次在兩盞燈之間添新路燈是隨機,并且每次添新路燈相互獨立.新添路燈與左右相鄰路燈的間隔都不小于10米是符合要求的,記符合要求的新添路燈數(shù)量為![]() ,則
,則![]() ( )
( )
A.30B.15C.10D.5
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點P為直線![]() 上任意一點,
上任意一點,![]() ,M為平面內(nèi)一點,且
,M為平面內(nèi)一點,且![]() .
.
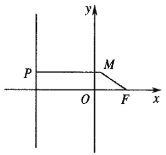
(Ⅰ)求點M的軌跡E的方程;
(Ⅱ)過點P作曲線E的切線,切點分別是![]() .若
.若![]() ,求點P的坐標.
,求點P的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),![]() ,已知函數(shù)
,已知函數(shù)![]() ,
,![]() .
.
(1)若函數(shù)![]() 有零點,求實數(shù)
有零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)對于![]() ,證明:當
,證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com