Question

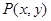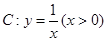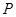點是曲線上的動點，曲線在點處的切線與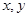軸分別交于兩點，點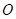是坐標原點.給出三個結論：①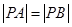;②△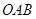的周長有最小值；③曲線上存在兩點，使得△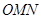為等腰直角三角形.其中正確結論的個數是

A．1

B．2

C．3

D．0

Answer 1

C

解析試題分析：設動點P(m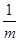，)（m＞0），則y^′=-，∴f^′(m)=-，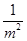
∴過動點P(m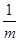，)的切線方程為：y-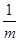=-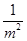(x-m)．
①分別令y=0，x=0，得A（2m，0），B(0，)．
則|PA|=，|PB|=，∴|PA|=|PB|，故①正確；
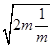②由上面可知：△OAB的周長=2m++2≥2×2+2=4+2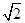，當且僅當m=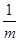，即m=1時取等號．故△OAB的周長有最小值4+2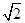，即②正確．
③假設曲線C上存在兩點M(a，)，N(b，)，不妨設0＜a＜b，∠OMN=90°．
則|ON|=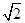|OM|，，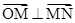
所以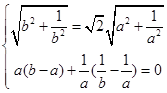
化為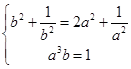，解得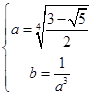，故假設成立．因此③正確．
故選C。
考點：本題主要考查導數的概念及應用；不等式的解法及應用。
點評：理解導數的幾何意義、基本不等式的性質、兩點間的距離公式及等腰直角三角形的性質是解題的關鍵．較難。