
【題目】定義在![]() 上的函數
上的函數![]() 的導函數為
的導函數為![]() ,且滿足
,且滿足![]() ,
, ![]() ,當
,當![]() 時有
時有![]() 恒成立,若非負實數
恒成立,若非負實數![]() 、
、![]() 滿足
滿足![]() ,
, ![]() ,則
,則![]() 的取值范圍為 .
的取值范圍為 .
【答案】![]()
【解析】試題分析:由y=f′(x)圖象可知,當x=0時,f′(x)=0,
當x∈(-∞,0)時,f′(x)<0,f(x)單調遞減,
當x∈(0,+∞)時,f′(x)>0,f(x)單調遞增,
又∵a,b為非負實數,
∴f(2a+b)≤1可化為f(2a+b)≤1=f(3),可得0≤2a+b≤3,
同理可得-2≤-a-2b≤0,即0≤a+2b≤2,
作出以及a≥0和b≥0所對應的平面區域,
得到如圖的陰影部分區域,
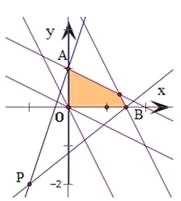
解之得A(0,1)和B(1.5,0)
而等于可行域內的點與P(-1,-2)連線的斜率,
結合圖形可知:kPB是最小值,kPA是最大值,
由斜率公式可得:kPA=3,kPB=![]() ,
,
故![]() 的取值范圍為
的取值范圍為![]()


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的方程是
的方程是![]() ,圓
,圓![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)分別求直線![]() 與圓
與圓![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() :
:![]() (
(![]() )與圓
)與圓![]() 的交點為
的交點為![]() 、
、![]() 兩點,與直線
兩點,與直線![]() 交于點
交于點![]() ,射線
,射線![]() :
:![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() 兩點,與直線
兩點,與直線![]() 交于點
交于點![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是從0,1,2,3四個數中任取的一個數,
是從0,1,2,3四個數中任取的一個數,![]() 是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
(2)若![]() 是從區間
是從區間![]() 任取的一個數,
任取的一個數,![]() 是從區間
是從區間![]() 任取的一個數,求上述方程有根的概率.
任取的一個數,求上述方程有根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-1《幾何證明選講》
已知A、B、C、D為圓O上的四點,直線DE為圓O的切線,AC∥DE,AC與BD相交于H點

(1)求證:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
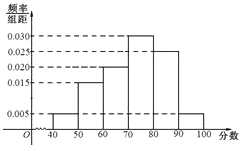
【題目】上周某校高三年級學生參加了數學測試,年部組織任課教師對這次考試進行成績分析.現從中抽取80名學生的數學成績(均為整數)的頻率分布直方圖如圖所示.
(Ⅰ)估計這次月考數學成績的平均分和眾數;
(Ⅱ)假設抽出學生的數學成績在![]() 段各不相同,且都超過94分.若將頻率視為概率,現用簡單隨機抽樣的方法,從95,96,97,98,99,100這6個數字中任意抽取2個數,有放回地抽取3次,記這3次抽取中恰好有兩名學生的數學成績的次數為
段各不相同,且都超過94分.若將頻率視為概率,現用簡單隨機抽樣的方法,從95,96,97,98,99,100這6個數字中任意抽取2個數,有放回地抽取3次,記這3次抽取中恰好有兩名學生的數學成績的次數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,橢圓C與y軸交于A、B兩點,|AB|=2.
,橢圓C與y軸交于A、B兩點,|AB|=2.
(Ⅰ)求橢圓C的方程;
(Ⅱ)已知點P是橢圓C上的動點,且直線PA,PB與直線x=4分別交于M、N兩點,是否存在點P,使得以MN為直徑的圓經過點(2,0)?若存在,求出點P的橫坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com