
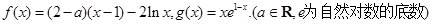
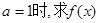 的單調區間;
的單調區間;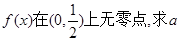 的最小值;
的最小值; ,使得
,使得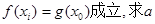 的取值范圍。
的取值范圍。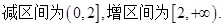 (II)
(II)
 使
使 成立。
成立。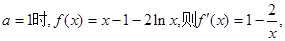 …………1分
…………1分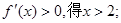 由
由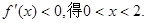
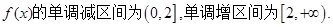 …………3分
…………3分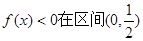 上恒成立不可能,
上恒成立不可能, 上無零點,只要對任意的
上無零點,只要對任意的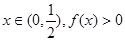 恒成立,
恒成立, 恒成立。 …………4分
恒成立。 …………4分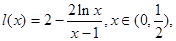
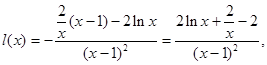 …………5分
…………5分
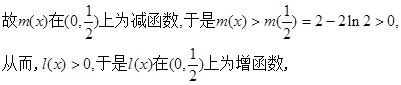
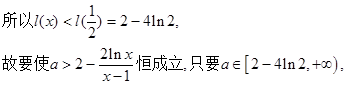

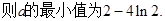 …………6分
…………6分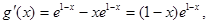
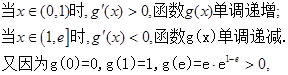
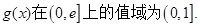 …………7分
…………7分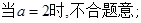
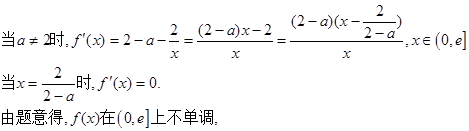
 ① …………9分
① …………9分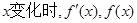 的變化情況如下:
的變化情況如下:| | 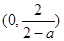 | 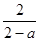 | 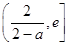 |
 | — | 0 | + |
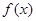 | | 最小值 | |

|
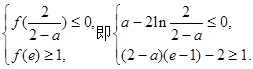
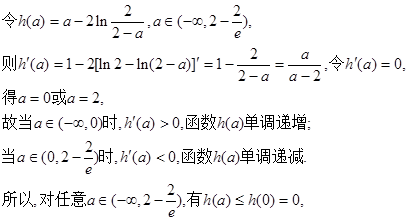
 恒成立。 …………10分
恒成立。 …………10分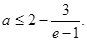 ④
④ 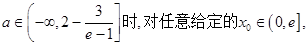
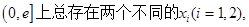
 成立
成立

 優等生題庫系列答案
優等生題庫系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com