
某校高三4班有50名學生進行了一場投籃測試,其中男生30人,女生20人.為了了解其投籃成績,甲、乙兩人分別都對全班的學生進行編號(1~50號),并以不同的方法進行數據抽樣,其中一人用的是系統抽樣,另一人用的是分層抽樣.若此次投籃考試的成績大于或等于80分視為優秀,小于80分視為不優秀,以下是甲、乙兩人分別抽取的樣本數據:
| 編號 | 性別 | 投籃成績 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 編號 | 性別 | 投籃成績 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
| | 優秀 | 非優秀 | 合計 |
| 男 | | | |
| 女 | | | |
| 合計 | | | 10 |
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
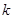 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
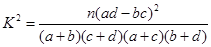 ,其中
,其中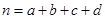 )
) (Ⅰ) =
= .
.
(Ⅱ)有95%以上的把握認為投籃成績與性別有關.
(Ⅲ)甲用的是系統抽樣,乙用的是分層抽樣. 采用分層抽樣方法比系統抽樣方法更優.
解析試題分析:(Ⅰ)首先明確“事件”記“兩名同學中恰有一名不優秀”為事件A,乙抽取的樣本數據中,男同學有4名優秀,記為a,b,c,d,2名不優秀,記為e,f .計算從男同學中抽取兩名,總的基本事件有15個,利用列舉法確定事件A包含的基本事件數為8,進一步得到 =
= . (Ⅱ)設投籃成績與性別無關,由乙抽取的樣本數據,得
. (Ⅱ)設投籃成績與性別無關,由乙抽取的樣本數據,得 列聯表,利用“卡方公式”,計算
列聯表,利用“卡方公式”,計算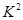 的觀測值并與臨界值表比較,得到結論.(Ⅲ)對照系統抽樣、分層抽樣的定義.確定抽樣方法,由(Ⅱ)的結論,并且從樣本數據能看出投籃成績與性別有明顯差異,得到結論.
的觀測值并與臨界值表比較,得到結論.(Ⅲ)對照系統抽樣、分層抽樣的定義.確定抽樣方法,由(Ⅱ)的結論,并且從樣本數據能看出投籃成績與性別有明顯差異,得到結論.
試題解析:(Ⅰ)記“兩名同學中恰有一名不優秀”為事件A,乙抽取的樣本數據中,男同學有4名優秀,記為a,b,c,d,2名不優秀,記為e,f . 1分
乙抽取的樣本數據,若從男同學中抽取兩名,則總的基本事件有15個, 2分
事件A包含的基本事件有 ,
, ,
, ,
, ,
,  ,
, ,
, ,
, ,共8個基本事件,所以
,共8個基本事件,所以  =
= . 4分
. 4分
(Ⅱ)設投籃成績與性別無關,由乙抽取的樣本數據,得 列聯表如下:
列聯表如下:
6分 優秀 非優秀 合計 男 4 2 6 女 0 4 4 合計 4 6 10 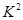 的觀測值
的觀測值
 4.444
4.444 3.841, 8分
3.841, 8分
所以有95%以上的把握認為投籃成績與性別有關. 9分
(Ⅲ)甲用的是系統抽樣,乙用的是分層抽樣. 10分
由(Ⅱ)的結論知,投籃成績與性別有關,并且從樣本數據能看出投籃成績與性別有明顯差異,因此采用分層抽樣方法比系統抽樣方法更優. 12分
考點:1、古典概型概率的計算,2、抽樣方法,3、“卡方公式”的應用.


科目:高中數學 來源: 題型:解答題
某校高三文科分為五個班.高三數學測試后, 隨機地在各班抽取部分學生進行成績統計,各班被抽取的學生人數恰好成等差數列,人數最少的班被抽取了18人.抽取出來的所有學生的測試成績統計結果的頻率分布條形圖如圖所示,其中120~130(包括120分但不包括130分)的頻率為0.05,此分數段的人數為5人.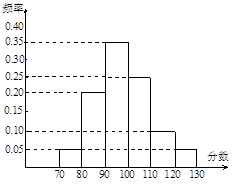
(1)問各班被抽取的學生人數各為多少人?
(2)在抽取的所有學生中,任取一名學生,求分數不小于90分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某企業員工500人參加“學雷鋒”志愿活動,按年齡分組:第1組 ,第2組
,第2組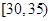 ,第3組
,第3組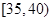 ,第4組
,第4組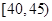 ,第5組
,第5組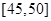 ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
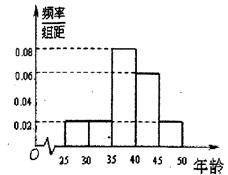
(1)上表是年齡的頻率分布表,求正整數 的值;
的值;
(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取6人,年齡在第1,2,3組的人數分別是多少?
(3)在(2)的前提下,從這6人中隨機抽取2人參加社區宣傳交流活動,求恰有1人年齡在第3組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
南昌市為增強市民的交通安全意識,面向全市征召“小紅帽”志愿者在部分交通路口協助交警維持交通,把符合條件的1000名志愿者按年齡分組:第1組 、第2組
、第2組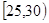 、第3組
、第3組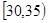 、第4組
、第4組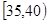 、第5組
、第5組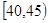 ,得到的頻率分布直方圖如圖所示:
,得到的頻率分布直方圖如圖所示:
(1)若從第3、4、5組中用分層抽樣的方法抽取12名志愿者在五一節這天到廣場協助交警維持交通,應從第3、4、5組各抽取多少名志愿者?
(2)在(1)的條件下,南昌市決定在這12名志愿者中在第四或第五組的志愿者中,隨機抽取3名志愿者到學校宣講交通安全知識,求到學校宣講交通知識的資源者中恰好1名市第五組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下表是某單位在2013年1—5月份用水量(單位:百噸)的一組數據:
月份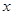 | 1 | 2 | 3 | 4 | 5 |
用水量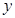 | 4 5 | 4 | 3 | 2 5 | 1 8 |
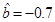 ,那么由該單位前4個月的數據中所得到的線性回歸方程預測5月份的用水量是否可靠?說明理由;
,那么由該單位前4個月的數據中所得到的線性回歸方程預測5月份的用水量是否可靠?說明理由;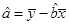 ,
,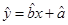
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某主任對全班50名學生的學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示
| | 積極參加班級工作 | 不太主動參加班級工作 |
| 學習積極性高 | 18 | 7 |
| 學習積極性一般 | 6 | 19 |
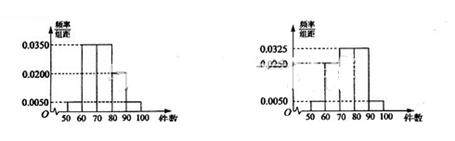
P(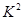 ≥k) ≥k) | 0.050 | 0.010 | 0.001 | 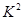 = =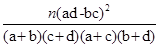 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了研究玉米品種對產量的影響,某農科院對一塊試驗田種植的一批玉米共10000 株的生長情況進行研究,現采用分層抽樣方法抽取50株作為樣本,統計結果如下:
| | 高莖 | 矮莖 | 合計 |
| 圓粒 | 11 | 19 | 30 |
| 皺粒 | 13 | 7 | 20 |
| 合計 | 24 | 26 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
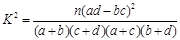 ,其中
,其中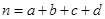 )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為研究工人的日平均生產量是否與年齡有關,現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,再將兩組工人的日平均生產件數分為5組: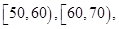
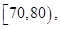
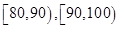 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.
(I)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的概率;
(II)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成列聯表,并判斷是否有90%的把握認為“生產能手與工人所在的年齡組有關”?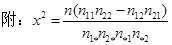
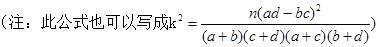
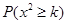 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某糖廠為了了解一條自動生產線上袋裝白糖的重量,隨機抽取了100袋,并稱出每袋白糖的重量(單位:g),得到如下頻率分布表。
| 分組 | 頻數 | 頻率 |
| [485.5,490.5) | 10 |  |
| [490.5,495.5) | 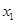 |  |
| [495.5,500.5) | 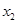 | 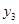 |
| [500.5,505.5] | 10 | |
| 合計 | 100 | |
 ,
, ,
,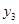 成等差數列。
成等差數列。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com