【題目】某市為了宣傳環保知識，舉辦了一次“環保知識知多少”的問卷調查活動（一
人答一份）．現從回收的年齡在20～60歲的問卷中隨機抽取了100份，統計結果如下面的圖表所示．
年齡 分組 | 抽取份數 | 答對全卷 的人數 | 答對全卷的人數 占本組的概率 |
[20,30) | 40 | 28 | 0．7 |
[30,40) |
| 27 | 0．9 |
[40,50) | 10 | 4 |
|
[50,60] | 20 |
| 0．1 |
（1）分別求出
， 
， 
， 
的值；
（2）從年齡在
答對全卷的人中隨機抽取2人授予“環保之星”，求年齡在
的人中至少有1人被授予“環保之星”的概率．
【答案】（1）
， 
， 
， 
；（2）
．
【解析】試題分析：（1）由抽取總問卷為100份可得
的值，由抽取份數為10份，答對全卷人數為4人可得
的值，由抽取份數為20份，答對全卷的人數占本組的概率為
可得
的值，由頻率分布直方圖中，各頻率之和等于1可得
的值；（2）利用列舉法寫出抽取2人授予“環保之星”的所有基本事件，并從中找出年齡在
的人中至少有1人被授予“環保之星”的基本事件，利用古典概型公式求出概率．
試題解析：（1）因為抽取總問卷為100份，所以
． 1分
年齡在
中，抽取份數為10份，答對全卷人數為4人，所以
． 2分
年齡在
中，抽取份數為20份，答對全卷的人數占本組的概率為
，
所以
，解得
． 3分
根據頻率直方分布圖，得
，
解得
． 4分
（2）因為年齡在
與
中答對全卷的人數分別為4人與2人．
年齡在
中答對全卷的4人記為
， 
， 
， 
，年齡在
中答對全卷的2人記為
， 
，則從這6人中隨機抽取2人授予“環保之星”獎的所有可能的情況是： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
共15種． 8分
其中所抽取年齡在
的人中至少有1人被授予“環保之星”的情況是： 
， 
， 
， 
， 
， 
， 
， 
， 
共9種． 11分
故所求的概率為
． 12分
科目：高中數學 來源： 題型：
【題目】為了解甲、乙兩廠產品的質量，從兩廠生產的產品中分別隨機抽取各10件樣品，測量產品中某種元素的含量（單位：毫克），如圖是測量數據的莖葉圖：
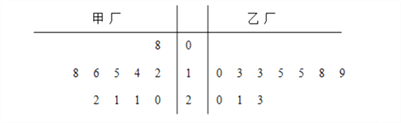
規定：當產品中的此種元素含量不小于16毫克時，該產品為優等品．
（1）從乙廠抽出的上述10件樣品中，隨機抽取3件，求抽到的3件樣品中優等品數
的分布列及其數學期望
；
（2）從甲廠的10件樣品中有放回地逐個隨機抽取3件，也從乙廠的10件樣品中有放回地逐個隨機抽取3件，求抽到的優等品數甲廠恰比乙廠多2件的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，已知曲線
的方程為
（
為參數），以坐標原點
為極點， 
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
（
）．
（1）求曲線
的普通方程和曲線
的直角坐標方程；
（2）曲線
上有3個點到曲線
的距離等于1，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】4月23日是世界讀書日，惠州市某中學在此期間開展了一系列的讀書教育活動。為了解本校學生課外閱讀情況，學校隨機抽取了100名學生對其課外閱讀時間進行調查。下面是根據調查結果繪制的學生日均課外閱讀時間(單位：分鐘)的頻率分布直方圖，且將日均課外閱讀時間不低于60分鐘的學生稱為“讀書迷”，低于60分鐘的學生稱為“非讀書迷”．
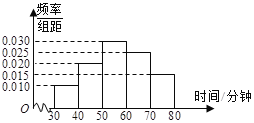
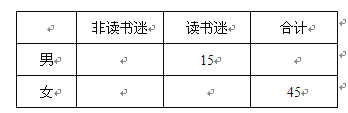
（Ⅰ）根據已知條件完成下面2×2列聯表，并據此判斷是否有99%的把握認為“讀書迷”與性別有關？
（Ⅱ）將頻率視為概率，現在從該校大量學生中用隨機抽樣的方法每次抽取1人，共抽取3次，記被抽取的3人中“讀書迷”的人數為
，若每次抽取的結果是相互獨立的，求
的分布列、數學期望
和方差
．
附：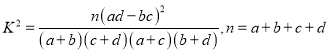 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“累積凈化量
”是空氣凈化器質量的一個重要衡量指標，它是指空氣凈化從開始使用到凈化效率為50%時對顆粒物的累積凈化量，以克表示，根據
《空氣凈化器》國家標準，對空氣凈化器的累計凈化量有如下等級劃分：
累積凈化量（克） |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器（共5000臺）的質量，隨機抽取
臺機器作為樣本進行估計，已知這臺機器的累積凈化量都分布在區間
中，按照
、
、
、
、
均勻分組，其中累積凈化量在的所有數據有：4.5,4.6,5.2,5.3,5.7和5.9，并繪制了頻率分布直方圖，如圖所示：
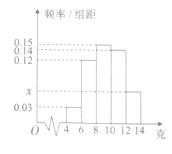
（1）求的值及頻率分布直方圖中
的值；
（2）以樣本估計總體，試估計這批空氣凈化器（共5000臺）中等級為
的空氣凈化器有多少臺？
（3）從累積凈化量在的樣本中隨機抽取2臺，求恰好有1臺等級為的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為調查某地區老人是否需要志愿者提供幫助，用簡單隨機抽樣方法從該地區調查了500位老年人，結果如下：
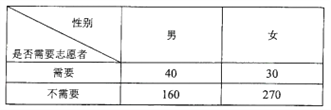
（Ⅰ）估計該地區老年人中，需要志愿者提供幫助的老年人的比例；
（Ⅱ）能否有
的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關？
（Ⅲ）根據（Ⅱ）的結論，能否提供更好的調查方法來估計該地區的老年人中，需要志愿者提供幫助的老年人的比例？說明理由.
附：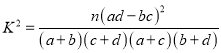 
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知城
和城
相距
，現計劃以
為直徑的半圓上選擇一點
（不與點
， 
重合）建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關，對城
和城
的總影響度為對城
與城
的影響度之和.記點到
城
的距離為
，建在
處的垃圾處理廠對城
和城
的總影響度為
.統計調查表明：垃圾處理廠對城
的影響度與所選地點到城
的距離的平方成反比例關系，比例系數為4；對城
的影響度與所選地點到城
的距離的平方成反比例關系，比例系數為
.當垃圾處理廠建在
的中點時，對城
和城
的總影響度為0.065.
（1）將
表示成
的函數.
（2）討論（1）中函數的單調性，并判斷在
上是否存在一點，使建在此處的垃圾處理廠對城
和城
的總影響度最小？若存在，求出該點到城
的距離；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
