
 的首項
的首項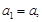 其中
其中 ,
, 令集合
令集合 .
. 是數列
是數列 中首次為1的項,請寫出所有這樣數列的前三項;
中首次為1的項,請寫出所有這樣數列的前三項; ;
; 時,求集合
時,求集合 中元素個數
中元素個數 的最大值.
的最大值.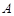 重元素個數
重元素個數 的最大值為21.
的最大值為21. 及
及 須討論
須討論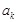 被3除余1,,
被3除余1,,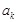 被3除余2,
被3除余2,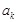 被3除余0,等三種情況.
被3除余0,等三種情況.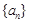 滿足:
滿足: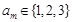 時,總有
時,總有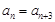 成立,其中
成立,其中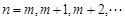 .
.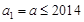 時,數列
時,數列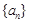 中大于3的各項:
中大于3的各項: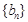 ,由(Ⅰ)可得
,由(Ⅰ)可得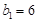 或9,
或9,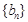 的項滿足:
的項滿足: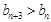 ,且當
,且當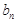 是3的倍數時,若使
是3的倍數時,若使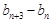 最小,需使
最小,需使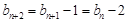 ,
,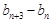 最小的數列
最小的數列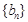 中,
中,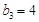 或7,且
或7,且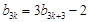 ,
,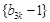 是首項為
是首項為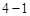 或
或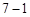 的公比為3的等比數列,應用等比數列的通項公式即可得出結論.
的公比為3的等比數列,應用等比數列的通項公式即可得出結論.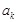 被3除余1,則由已知可得
被3除余1,則由已知可得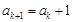 ,
,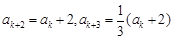 ;
;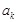 被3除余2,則由已知可得
被3除余2,則由已知可得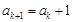 ,
,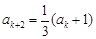 ,
,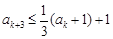 ;
;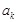 被3除余0,則由已知可得
被3除余0,則由已知可得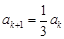 ,
,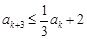 ;
;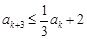 ,
,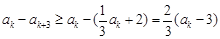
 中的任意一項
中的任意一項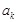 ,“若
,“若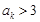 ,則
,則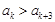 ”.
”.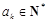 ,所以
,所以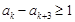 .
. 中必存在某一項
中必存在某一項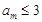 (否則會與上述結論矛盾!)
(否則會與上述結論矛盾!)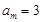 ,則
,則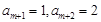 ;若
;若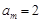 ,則
,則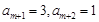 ,若
,若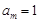 ,則
,則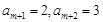 ,
, . 8分
. 8分 中元素個數
中元素個數 的最大值為21.
的最大值為21.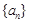 滿足:
滿足: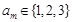 時,總有
時,總有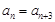 成立,其中
成立,其中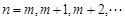 .
.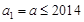 時,數列
時,數列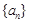 中大于3的各項:
中大于3的各項: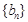 ,由(I)可得
,由(I)可得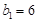 或9,
或9,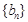 的項滿足:
的項滿足: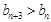 ,且當
,且當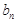 是3的倍數時,若使
是3的倍數時,若使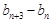 最小,需使
最小,需使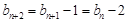 ,
,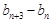 最小的數列
最小的數列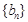 中,
中,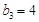 或7,且
或7,且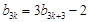 ,
,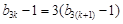 ,所以數列
,所以數列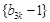 是首項為
是首項為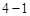 或
或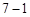 的公比為3的等比數列,
的公比為3的等比數列,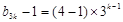 或
或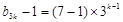 ,即
,即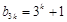 或
或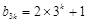 ,
,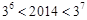 ,所以,當
,所以,當 時,
時,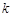 的最大值是6,
的最大值是6, ,所以集合
,所以集合 重元素個數
重元素個數 的最大值為21. 13分
的最大值為21. 13分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com