Question

【題目】在平面直角坐標系中，橢圓的離心率為,直線被橢圓截得的線段長為.

（1）求橢圓的方程；

（2）過原點的直線與橢圓交于兩點（不是橢圓的頂點），點在橢圓上，且，直線與軸軸分別交于兩點.

①設直線斜率分別為，證明存在常數使得，并求出的值；

②求面積的最大值.

Answer 1

【答案】(1).

(2) ①證明見解析，；②.

【解析】試題分析：（1）首先由題意得到，即.

將代入可得，

由，可得.得解.

（2）（ⅰ）注意從確定的表達式入手，探求使成立的.

設，則，

得到，

根據直線BD的方程為，

令，得，即.得到.

由，作出結論.

（ⅱ）直線BD的方程，

從確定的面積表達式入手，應用基本不等式得解.

試題解析：（1）由題意知，可得.

橢圓C的方程可化簡為.

將代入可得，

因此，可得.

因此，

所以橢圓C的方程為.

（2）（ⅰ）設，則，

因為直線AB的斜率，

又，所以直線AD的斜率，

設直線AD的方程為，

由題意知，

由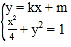，可得.

所以，

因此，

由題意知，

所以，

所以直線BD的方程為，

令，得，即.

可得.

所以，即.

因此存在常數使得結論成立.

（ⅱ）直線BD的方程，

令，得，即，

由（ⅰ）知，

可得的面積，

因為，當且僅當時等號成立，

此時S取得最大值，

所以的面積的最大值為.