
【題目】設函數![]() (
(![]() 且
且![]() )是奇函數.
)是奇函數.
(1)求常數![]() 的值;
的值;
(2)若![]() ,試判斷函數
,試判斷函數![]() 的單調性,并加以證明;
的單調性,并加以證明;
(3)若![]() ,且函數
,且函數![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() ,求實數
,求實數![]() 的值.
的值.
 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足f(x﹣1)的對稱軸為x=1,f(x+1)= ![]() (f(x)≠0),且在區間(1,2)上單調遞減,已知α、β是鈍角三角形中兩銳角,則f(sinα)和f(cosβ)的大小關系是( )
(f(x)≠0),且在區間(1,2)上單調遞減,已知α、β是鈍角三角形中兩銳角,則f(sinα)和f(cosβ)的大小關系是( )
A.f(sinα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(sinα)=f(cosβ)
D.以上情況均有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明:“活水圍網”養魚時,某種魚在一定的條件下,每尾魚的平均生長速度![]() (單位:千克/年)是養殖密度
(單位:千克/年)是養殖密度![]() (單位:尾/立方米)的函數.當
(單位:尾/立方米)的函數.當![]() 不超過
不超過![]() 尾/立方米時,
尾/立方米時, ![]() 的值為
的值為![]() 千克/年;當
千克/年;當![]() 時,
時, ![]() 是
是![]() 的一次函數,且當
的一次函數,且當![]() 時,
時, ![]() .
.
(![]() )當
)當![]() 時,求
時,求![]() 關于
關于![]() 的函數的表達式.
的函數的表達式.
(![]() )當養殖密度
)當養殖密度![]() 為多大時,每立方米的魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
為多大時,每立方米的魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=xex , 則( )
A.x=1為f(x)的極大值點
B.x=1為f(x)的極小值點
C.x=﹣1為f(x)的極大值點
D.x=﹣1為f(x)的極小值點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據第2題求出的回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
查看答案和解析>>
科目:高中數學 來源: 題型:
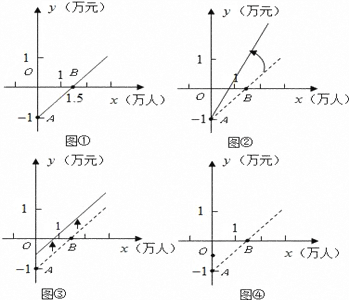
【題目】如圖是某公共汽車線路收支差額(票價總收人減去運營成本)與乘客量的函數圖象.目前這條線路虧損,為了扭虧,有關部門舉行提高票價的聽證會.乘客代表認為:公交公司應節約能源,改善管理,降低運營成本,以此舉實現扭虧.公交公司認為:運營成本難以下降,公司己盡力,提高票價才能扭虧.根據這兩種意見,可以把圖分別改畫成圖②和圖③,
(1)說明圖①中點![]() 和點
和點![]() 以及射線
以及射線![]() 的實際意義;
的實際意義;
(2)你認為圖②和圖③兩個圖象中,反映乘客意見的是_________,反映公交公司意見的是_________.
(3)如果公交公司采用適當提高票價又減少成本的辦法實現扭虧為贏,請你在圖④中畫出符合這種辦法的大致函數關系圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+bx2+cx+d的圖象如圖,則函數 ![]() 的單調遞減區間是( )
的單調遞減區間是( ) 
A.(﹣∞,﹣2)
B.(﹣∞,1)
C.(﹣2,4)
D.(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學對高三學生進行體能測試,已知高三某文科班有學生30人,立定跳遠的測試成績用莖葉圖表示如圖(單位: ![]() );男生成績在
);男生成績在![]() 以上(包括
以上(包括![]() )定義為“合格”,成績在
)定義為“合格”,成績在![]() 以下(不包括
以下(不包括![]() )定義為“不合格”;女生成績在
)定義為“不合格”;女生成績在![]() 以上(包括
以上(包括![]() )定義為“合格”,成績在
)定義為“合格”,成績在![]() 以下(不包括
以下(不包括![]() )定義為“不合格.
)定義為“不合格.

(1)求女生立定跳遠測試成績的中位數;
(2)若在男生中按成績是否合格進行分層抽樣,抽取6人,求抽取成績為“合格”的學生人數;
(3)若從(2)中抽取的6名男生中任意選取4人,求這4人中至少有3人“合格”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com