
如圖所示,在四棱錐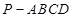 中,底面
中,底面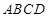 為矩形,
為矩形,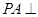 平面
平面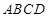 ,點
,點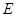 在線段
在線段 上,
上,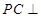 平面
平面 .
.
(1)證明: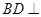 平面
平面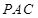 .;
.;
(2)若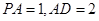 ,求三棱錐
,求三棱錐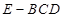 的體積.
的體積.
(1)見解析(2)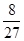
解析試題分析:(1)要證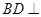 平面
平面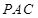 ,需證
,需證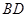 與平面
與平面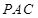 內的兩條相交直線都垂直,
內的兩條相交直線都垂直,
由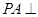 平面
平面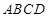 ,可證
,可證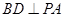 ,由
,由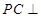 平面
平面 ,可證
,可證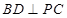 .根據線面垂直的判定定理,
.根據線面垂直的判定定理,
可證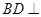 平面
平面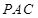 .(2)設矩形
.(2)設矩形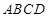 的對角線的交點為
的對角線的交點為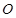 ,連結
,連結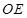 ,由(1)的結論可知
,由(1)的結論可知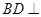 平面
平面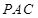 ,從而有
,從而有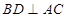 ,所以矩形
,所以矩形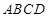 為正方形,邊長為2;由
為正方形,邊長為2;由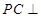 平面
平面 ,知
,知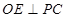 ,因此
,因此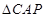 與
與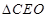 相似,可確定
相似,可確定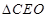 的各邊長,然后由
的各邊長,然后由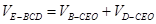 求三棱錐
求三棱錐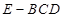 的體積.
的體積.
試題解析:(1)∵PA⊥平面ABCD,
∴PA⊥BD.
∵PC⊥平面BDE,
∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC. 6分
(2)如圖,設AC與BD的交點為O,連結OE.
∵PC⊥平面BDE,∴PC⊥OE.
由(1)知,BD⊥平面PAC,∴BD⊥AC,
由題設條件知,四邊形ABCD為正方形.
由AD=2,得AC=BD=2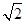 ,OC=
,OC=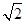 .
.
在Rt△PAC中,PC=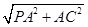 =
=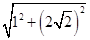 =3.
=3.
易知Rt△PAC∽Rt△OEC,
∴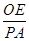 =
=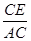 =
=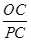 ,即
,即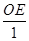 =
=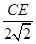 =
=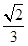 ,∴OE=
,∴OE=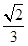 ,CE=
,CE=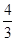 .
.
∴VE-BCD=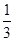 S△CEO·BD=
S△CEO·BD=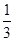 ·
·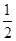 OE·CE·BD=
OE·CE·BD=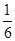 ·
·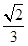 ·
·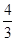 ·2
·2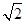 =
=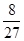 . 13分
. 13分
考點:1、直線與平面垂直的判定與性質;2、棱錐的體積.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
如圖(1)所示,△ABC是等腰直角三角形,AC=BC=4,E、F分別為AC、AB的中點,將△AEF沿EF折起,使A′在平面BCEF上的射影O恰為EC的中點,得到圖(2).
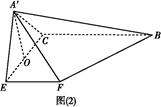
(1)求證:EF⊥A′C;
(2)求三棱錐F A′BC的體積.
A′BC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在邊長為4的菱形ABCD中,∠DAB=60°,點E、F分別在邊CD、CB上,點E與點C、D不重合,EF⊥AC,EF∩AC=O,沿EF將△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.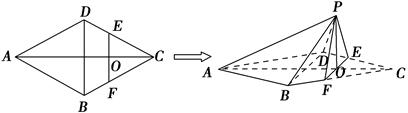
(1)求證:BD⊥平面POA;
(2)記三棱錐PABD體積為V1,四棱錐PBDEF體積為V2,且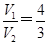 ,求此時線段PO的長.
,求此時線段PO的長.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,四邊形ABCD是邊長為2的正方形,直線l與平面ABCD平行,E和F是l上的兩個不同點,且EA=ED,FB=FC.E′和F′是平面ABCD內的兩點,EE′和FF′都與平面ABCD垂直.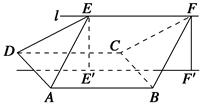
(1)證明:直線E′F′垂直且平分線段AD;
(2)若∠EAD=∠EAB=60 °,EF=2.求多面體ABCDEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在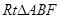 中,AB=2BF=4,C,E分別是AB,AF的中點(如下左圖).將此三角形沿CE對折,使平面AEC⊥平面BCEF(如下右圖),已知D是AB的中點.
中,AB=2BF=4,C,E分別是AB,AF的中點(如下左圖).將此三角形沿CE對折,使平面AEC⊥平面BCEF(如下右圖),已知D是AB的中點.
(1)求證:CD∥平面AEF;
(2)求證:平面AEF⊥平面ABF;
(3)求三棱錐C-AEF的體積,
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示的幾何體ABCDFE中,△ABC,△DFE都是等邊三角形,且所在平面平行,四邊形BCED是邊長為2的正方形,且所在平面垂直于平面ABC.
(Ⅰ)求幾何體ABCDFE的體積;
(Ⅱ)證明:平面ADE∥平面BCF;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com