
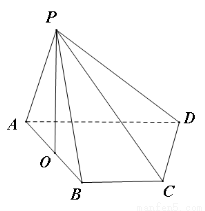
如圖,四棱錐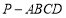 的底面
的底面 是直角梯形,
是直角梯形,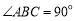 ,
,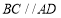 ,且
,且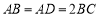 ,頂點
,頂點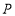 在底面
在底面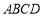 內的射影恰好落在
內的射影恰好落在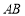 的中點
的中點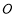 上.
上.
(1)求證: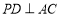 ;
;
(2)若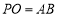 ,求直線
,求直線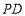 與
與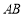 所成角的 余弦值;
所成角的 余弦值;
(3)若平面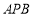 與平面
與平面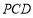 所成的二面角為
所成的二面角為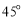 ,求
,求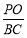 的值.
的值.
(1)詳見解析;(2)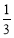 ;(3)
;(3) .
.
【解析】
試題分析:(1)以O為坐標原點,AB所在直線為x軸,OP所在直線為z軸,建立空間直角坐標系o-xyz,求出向量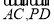 ,的坐標,代入數量積公式,驗證其數量積與0的關系,即可得到結論.
,的坐標,代入數量積公式,驗證其數量積與0的關系,即可得到結論.
(2)由PO=BC,得h=a,求出向量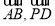 ,的坐標,代入向量夾角公式,即可求出直線PD與AB所成的角;
,的坐標,代入向量夾角公式,即可求出直線PD與AB所成的角;
(3)求出平面APB與平面PCD的法向量,根據平面APB與平面PCD所成的角為60°,構造關于h的方程,解方程即可得到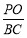 的值.
的值.
試題解析:因為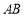 中點
中點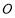 為點
為點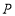 在平面
在平面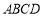 內的射影,所以
內的射影,所以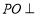 平面
平面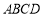 .過
.過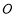 作
作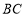 的平行線交
的平行線交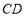 與點
與點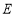 ,則
,則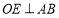 .
.
建立如圖所示的空間直角坐標系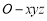 2分
2分
(1)設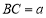 ,
,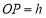 ,則
,則
 ,
,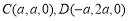 .
.
∴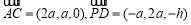 .
.
∵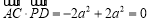 , ∴
, ∴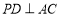 . 6分
. 6分
(2)由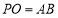 ,得
,得 ,于是
,于是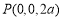
∵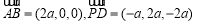 , 8分
, 8分
∴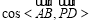

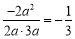 ,
,
∴直線PD與AB所成的角的余弦值為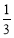 . 10分
. 10分
(3)設平面PAB的法向量為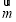 ,可得
,可得 ,
,
設平面PCD的法向量為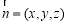 ,
,
由題意得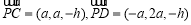 ,
,
∵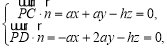 ∴
∴ 令
令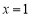 ,得到
,得到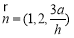 , 12分
, 12分
∴ , 14分
, 14分
∵平面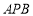 與平面
與平面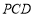 所成的二面角為
所成的二面角為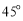 ,∴
,∴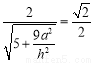 ,解得
,解得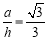 ,
,
即 . 16分
. 16分
考點:(1)直線與平面所成的角;(2)異面直線及其所成的角.


 智慧小復習系列答案
智慧小復習系列答案科目:高中數學 來源:2015屆江西南昌市四校高二上學期期末聯考文科數學試卷(解析版) 題型:選擇題
矩形ABCD中,點E為邊CD的中點,若在矩形ABCD內部隨機取一個點Q,則點Q取自△ABE的概率等于( )
A.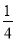 B.
B.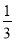 C.
C.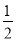 D.
D.
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇省常州市高二上學期期末考試理科數學試卷(解析版) 題型:填空題
已知橢圓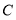 :
: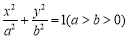 的短軸長為2,離心率為
的短軸長為2,離心率為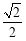 ,設過右焦點的直線
,設過右焦點的直線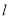 與橢圓
與橢圓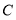 交于不同的兩點A,B,過A,B作直線
交于不同的兩點A,B,過A,B作直線 的垂線AP,BQ,垂足分別為P,Q.記
的垂線AP,BQ,垂足分別為P,Q.記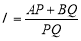 , 若直線l的斜率
, 若直線l的斜率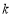 ≥
≥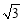 ,則
,則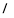 的取值范圍為 .
的取值范圍為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com