
【題目】已知函數![]() .
.
(1)當![]() 時,證明函數
時,證明函數![]() 在
在![]() 是單調函數;
是單調函數;
(2)當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)設![]() ,
,![]() 是函數
是函數![]() 圖象上任意不同的兩點,記線段
圖象上任意不同的兩點,記線段![]() 的中點的橫坐標是
的中點的橫坐標是![]() ,證明直線
,證明直線![]() 的斜率
的斜率![]()
![]() .
.
【答案】(1)證明見解析;(2)![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】試題分析:
(1)首先求解導函數,由![]() 可得函數
可得函數![]() 在
在![]() 是單增函數;
是單增函數;
(2)利用函數的單調性結合題意得到關于實數a的方程,解方程可得![]() .
.
(3)首先求得斜率的表達式,然后結合表達式設![]() ,構造新函數
,構造新函數![]() ,結合函數的特征即可證得結論.
,結合函數的特征即可證得結論.
試題解析:
(1)解:![]() .
.
因為![]() ,
,![]() ,所以
,所以![]() .∴函數
.∴函數![]() 在
在![]() 是單增函數;
是單增函數;
(2)解:在![]() 上,分如下情況討論:
上,分如下情況討論:
1.當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,其最小值為
單調遞增,其最小值為![]() ,這與函數在
,這與函數在![]() 上的最小值是
上的最小值是![]() 相矛盾;
相矛盾;
2.當![]() 時,函數
時,函數![]() 在
在![]() 單調遞增,其最小值為
單調遞增,其最小值為![]() ,同樣與最小值是相矛盾;
,同樣與最小值是相矛盾;
3.當![]() 時,函數
時,函數![]() 在
在![]() 上有
上有![]() ,單調遞減,在
,單調遞減,在![]() 上有
上有![]() ,單調遞增,
,單調遞增,
∴函數![]() 的最小值為
的最小值為![]() ,得
,得![]() .
.
(3)證明:當![]() 時,
時,![]() ,
,![]() .
.
又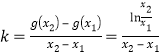 ,不妨設
,不妨設![]() ,
,
要比較![]() 與
與![]() 的大小,即比較
的大小,即比較![]() 與
與![]() 的大小,又因為
的大小,又因為![]() ,
,
所以即比較![]() 與
與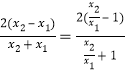 的大小.
的大小.
令![]() ,則
,則![]() ∴
∴![]() 在
在![]() 上是增函數.
上是增函數.
又![]() ,∴
,∴![]() ,
,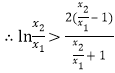 ,即
,即![]() .
.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】某品牌手機銷售商今年1,2,3月份的銷售量分別是1萬部,1.2萬部,1.3萬部,為估計以后每個月的銷售量,以這三個月的銷售為依據,用一個函數模擬該品牌手機的銷售量y(單位:萬部)與月份x之間的關系,現從二次函數![]() 或函數
或函數![]() 中選用一個效果好的函數行模擬,如果4月份的銷售量為1.37萬件,則5月份的銷售量為__________萬件.
中選用一個效果好的函數行模擬,如果4月份的銷售量為1.37萬件,則5月份的銷售量為__________萬件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,且當
上的奇函數,且當![]() 時,
時, ![]() ;
;
(1)求函數![]() 在
在![]() 上的解析式并畫出函數
上的解析式并畫出函數![]() 的圖象(不要求列表描點,只要求畫出草圖)
的圖象(不要求列表描點,只要求畫出草圖)
(2)(ⅰ)寫出函數![]() 的單調遞增區間;
的單調遞增區間;
(ⅱ)若方程![]() 在
在![]() 上有兩個不同的實數根,求實數
上有兩個不同的實數根,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 與
與![]() 軸的正半軸相交于點
軸的正半軸相交于點![]() ,點
,點![]() 為橢圓的焦點,且
為橢圓的焦點,且![]() 是邊長為2的等邊三角形,若直線
是邊長為2的等邊三角形,若直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() .
.
(1)直線![]() 的斜率之積是否為定值?若是,請求出該定值;若不是,請說明理由;
的斜率之積是否為定值?若是,請求出該定值;若不是,請說明理由;
(2)求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有4個不同的球,4個不同的盒子,把球全部放入盒子內.
(1)共有幾種放法?
(2)恰有1個空盒,有幾種放法?
(3)恰有2個盒子不放球,有幾種放法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張師傅想要一個如圖1所示的鋼筋支架的組合體,來到一家鋼制品加工店定制,拿出自己畫的組合體三視圖(如圖2所示).店老板看了三視圖,報了最低價,張師傅覺得很便宜,當即甩下定金和三視圖,約定第二天提貨.第二天提貨時,店老板一臉壞笑的捧出如圖3–1所示的組合體,張師傅一看,臉都綠了:“奸商,怎能如此偷工減料”.店老板說,我是按你的三視圖做的,要不我給你加一個正方體,但要加價,隨機加上了一個正方體,得到如圖3–2所示的組合體;張師傅臉還是綠的,店老板又加上一個正方體,組成了如圖 3–3 所示的組合體,又加價;張師傅臉繼續綠,店老板再加一個正方體,組成如圖 3–4 所示的組合體,再次加價;雙方就三視圖爭吵不休……
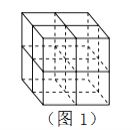
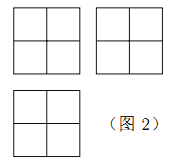
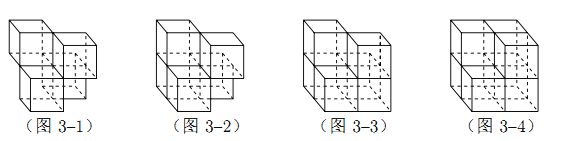
你認為店老板提供的![]() 個組合體的三視圖與張師傅畫的三視圖一致的個數是( )
個組合體的三視圖與張師傅畫的三視圖一致的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com