【題目】下列是有關三角形ABC的幾個命題，
①若tanA+tanB+tanC＞0，則△ABC是銳角三角形；
②若sin2A=sin2B，則△ABC是等腰三角形；
③若（ 
+ 
） 
=0，則△ABC是等腰三角形；
④若cosA=sinB，則△ABC是直角三角形；
其中正確命題的個數是（ ）
A..1
B..2
C.3
D.4
【答案】B
【解析】解：①∵tanA+tanB=tan（A+B）（1﹣tanAtanB），
∴tanA+tanB+tanC=tan（A+B）（1﹣tanAtanB）+tanC=tanAtanBtanC＞0，
∴A，B，C是△ABC的內角，故內角都是銳角，故①正確；
②∵sin2A=sin2B
∴sin2A﹣sin2B=cos（A+B）sin（A﹣B）=0
∴cos（A+B）=0或sin（A﹣B）=0
∴A+B= 
或A=B，
若sin2A=sin2B，則△ABC是等腰三角形或是直角三角形；故②錯誤
③若（ 
+ 
） 
=0，
則（ + ）（ ﹣ ）=0，
即| |2﹣| |2=0，
則| |2=| |2 ， 即| |=| |，
則AB=AC，則△ABC是等腰三角形；正確，故③正確，
④若cosA=sinB，則sinB=cosA=sin（ 
），∴ 
，
即A+B= 或B﹣A= ，則△ABC不一定為直角三角形，故④錯誤，
故選：B
【考點精析】本題主要考查了命題的真假判斷與應用的相關知識點，需要掌握兩個命題互為逆否命題，它們有相同的真假性；兩個命題為互逆命題或互否命題，它們的真假性沒有關系才能正確解答此題．
科目：高中數學 來源： 題型：
【題目】如圖，記長方體ABCD﹣A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的幾何體為Ω，則下列結論中不正確的是（ ）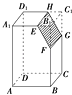 
A.EH∥FG
B.四邊形EFGH是平行四邊形
C.Ω是棱柱
D.Ω是棱臺
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
=1（a＞b＞0）的離心率為 
，且點 
在該橢圓上
（1）求橢圓C的方程；
（2）過橢圓C的左焦點F1的直線l與橢圓相交于A，B兩點，若△AOB的面積為 
，求圓心在原點O且與直線l相切的圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）= 
sin（ωx+φ）﹣cos（ωx+φ）（0＜φ＜π，ω＞0）對任意x∈R，都有f（﹣x）+f（x）=0，f（x）+f（x+ 
）=0，則f（ 
）=（ ）
A.0
B.1
C.
D.2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱ABC﹣A1B1C1中，側棱垂直于底面，AB⊥BC，AA1=AC=2，BC=1，E，F分別是A1C1 ， BC的中點．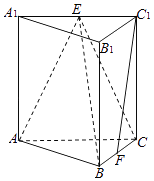 
（1）求證：AB⊥C1F；
（2）求證：C1F∥平面ABE；
（3）求三棱錐E﹣ABC的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設向量 
=（sinx，cosx）， 
=（cosx，sinx），x∈R，函數f（x）= （ ﹣ ）．
（1）求函數f（x）的最小正周期；
（2）當x∈[- 
， ]時，求函數f（x）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有以下四種變換方式：
① 向左平移
個單位長度，再將每個點的橫坐標縮短為原來的
;
② 向右平移
個單位長度，再將每個點的橫坐標縮短為原來的;
③ 每個點的橫坐標縮短為原來的，向右平移個單位長度;
④ 每個點的橫坐標縮短為原來的，向左平移個單位長度;
其中能將
的圖像變換成函數
的圖像的是（ ）
A.①和③ B.①和④ C.②和④ D.②和③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
， 
），且對任意
，都有
.
（Ⅰ）用含
的表達式表示
；
（Ⅱ）若
存在兩個極值點
， 
，且
，求出
的取值范圍，并證明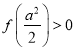
；
（Ⅲ）在（Ⅱ）的條件下，判斷
零點的個數，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
