【題目】在正方體ABCD﹣A1B1C1D1中，B1C與對角面DD1B1B所成角的大小是（ ）
A.15°
B.30°
C.45°
D.60°
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】計算題。
（1）已知等比數列{an}中，a1=﹣1，a4=64，求q與S4
（2）已知等差數列{an}中，a1= 
，d=﹣ 
，Sn=﹣15，求n及an ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場擬對某商品進行促銷，現有兩種方案供選擇，每種促銷方案都需分兩個月實施，且每種方案中第一個月與第二個月的銷售相互獨立.根據以往促銷的統計數據，若實施方案1，預計第一個月的銷量是促銷前的1.2倍和1.5倍的概率分別是0.6和0.4，第二個月的銷量是第一個月的1.4倍和1.6倍的概率都是0.5；若實施方案2，預計第一個月的銷量是促銷前的1.4倍和1.5倍的概率分別是0.7和0.3，第二個月的銷量是第一個月的1.2倍和1.6倍的概率分別是0.6和0.4.令
表示實施方案
的第二個月的銷量是促銷前銷量的倍數.
（Ⅰ）求
， 
的分布列；
（Ⅱ）不管實施哪種方案， 
與第二個月的利潤之間的關系如下表，試比較哪種方案第二個月的利潤更大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的首項a1=a，Sn是數列{an}的前n項和，且滿足：Sn2=3n2an+Sn﹣12 ， an≠0，n≥2，n∈N* ．
（1）若數列{an}是等差數列，求a的值；
（2）確定a的取值集合M，使a∈M時，數列{an}是遞增數列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體中，四邊形AA1B1B是邊長為3的正方形，CC1=2，CC1∥AA1 ， 這個幾何體是棱柱嗎？若是，指出是幾棱柱．若不是棱柱，請你試用一個平面截去一部分，使剩余部分是一個棱長為2的三棱柱，并指出截去的幾何體的特征，在立體圖中畫出截面．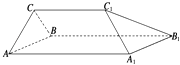 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
（
）
（Ⅰ）討論
的單調性；
（Ⅱ）證明：當
時，函數
（
）有最小值.記
的最小值為
，求
的值域；
（Ⅲ）若
存在兩個不同的零點
， 
（
），求
的取值范圍，并比較
與0的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
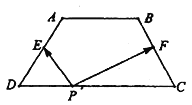
【題目】如圖，梯形
中， 
， 
， 
， 
, 
和
分別為
與
的中點，對于常數
，在梯形
的四條邊上恰好有8個不同的點
，使得
成立，則實數
的取值范圍是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】電視傳媒公司為了解某地區電視觀眾對某類體育節目的收視情況，隨機抽取了100名觀眾進行調查.下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖：
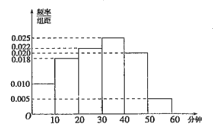
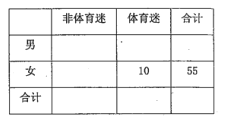
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
（1）根據已知條件完成上面的
列聯表，若按
的可靠性要求，并據此資料，你是否認為“體育迷”與性別有關？
（2）將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中，采用隨機抽樣方法每次抽取1名觀眾，抽取3次，記被抽取的3名觀眾中的“體育迷”人數為
.若每次抽取的結果是相互獨立的，求
分布列，期望
和方差
.
附：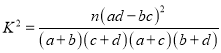 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
