【題目】
（1）求對稱軸是 
軸，焦點在直線 
上的拋物線的標準方程；
（2）過拋物線 
焦點 
的直線 
它交于 
兩點，求弦 
的中點的軌跡方程.
【答案】
（1）解：對稱軸是 
軸則頂點在焦點在 軸
所以 
，則 
， 
，
.
（2）解：由題知拋物線焦點為 
，
當直線的斜率存在時，設為 
，則焦點弦方程為 
，
代入拋物線方程得所以 
，由題意知斜率不等于0，
方程是一個一元二次方程，由韋達定理： 
所以中點坐標： 
代入直線方程
中點縱坐標； 
即中點為 
消參數(shù) ，得其方程為 
當直線的斜率不存在時，直線的中點是 ，符合題意，
故答案為: .
【解析】(1)先求出拋物線的焦點坐標,再求拋物線的方程;
(2)設出過焦點的直線的方程代入到拋物線方程中,消去y得關(guān)于x的一元二次方程,結(jié)合 韋達定理,表示出弦中點的坐標,消去參數(shù)k得中點軌跡方程.
科目：高中數(shù)學 來源： 題型：
【題目】某保險公司有一款保險產(chǎn)品的歷史收益率（收益率=利潤÷保費收入）的頻率分布直方圖如圖所示：
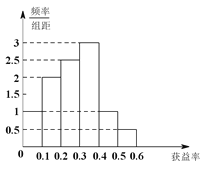
（Ⅰ）試估計平均收益率；
（Ⅱ）根據(jù)經(jīng)驗，若每份保單的保費在20元的基礎(chǔ)上每增加
元，對應的銷量
（萬份）與
（元）有較強線性相關(guān)關(guān)系，從歷史銷售記錄中抽樣得到如下5組
與
的對應數(shù)據(jù)：
據(jù)此計算出的回歸方程為
.
（i）求參數(shù)
的估計值；
（ii）若把回歸方程
當作
與
的線性關(guān)系，用（Ⅰ）中求出的平均收益率估計此產(chǎn)品的收益率，每份保單的保費定為多少元時此產(chǎn)品可獲得最大收益，并求出該最大收益.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在△ABC中，內(nèi)角A,B,C所對應的邊分別為a,b,c，且 
.
（1）求角B的大小；
（2）若b= 
，求△ABC的面積的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)y=f(x)，f(0)=-2，且對 
，y 
R，都有f(x+y)-f(y)=(x+2y+1)x.
（1）求f(x)的表達式；
（2）已知關(guān)于x的不等式f(x)-ax+a+1 
的解集為A，若A[2,3]，求實數(shù)a的取值范圍；
（3）已知數(shù)列{ 
}中， 
， 
，記 
，且數(shù)列{ 
的前n項和為 
，
求證： 
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知在△ABC中，角A，B，C所對的邊分別是a，b，c，且a、b、c成等比數(shù)列，c= 
bsinC﹣ccosB．
（Ⅰ）求B的大小；
（Ⅱ）若b=2 ，求△ABC的周長和面積．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知以點
為圓心的圓過點
和
，線段
的垂直平分線交圓于點
、
，且
,
（1）求直線
的方程； （2）求圓的方程。
（3）設點
在圓上，試探究使
的面積為 8 的點共有幾個？證明你的結(jié)論
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓C： 
+ 
=1（a＞b＞0）的離心率為 
，點B是橢圓C的上頂點，點Q在橢圓C上（異于B點）．
（Ⅰ）若橢圓V過點（﹣ 
， ），求橢圓C的方程；
（Ⅱ）若直線l：y=kx+b與橢圓C交于B、P兩點，若以PQ為直徑的圓過點B，證明：存在k∈R， 
= 
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
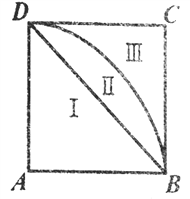
【題目】如圖，
是正方形
的對角線，弧
的圓心是
，半徑為
，正方形以為軸旋轉(zhuǎn)，求圖中Ⅰ，Ⅱ，Ⅲ三部分旋轉(zhuǎn)所得旋轉(zhuǎn)體的體積之比.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
