
已知函數
(1)若 ,有
,有 ,求
,求 的取值范圍;
的取值范圍;
(2)當 有實數解時,求
有實數解時,求 的取值范圍。
的取值范圍。
(1)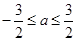 ;(2)
;(2)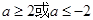 。
。
解析試題分析:(1)設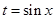 ,則原函數變形為
,則原函數變形為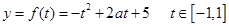 其對稱軸為
其對稱軸為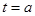 。
。
①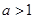 時,函數在
時,函數在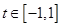 上單調遞增,所以函數值域為
上單調遞增,所以函數值域為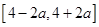 。因此有
。因此有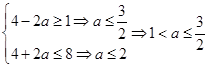
②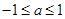 時,有
時,有 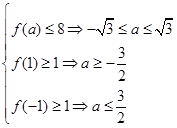 ,所以
,所以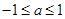 .
.
③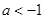 時,函數在
時,函數在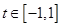 上單調遞減,有
上單調遞減,有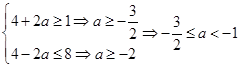
綜上所述: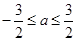
(2)①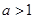 時,函數在
時,函數在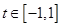 上單調遞增,因此有
上單調遞增,因此有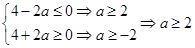
②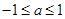 時,有
時,有 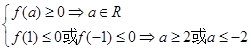 ,所以此時無解。
,所以此時無解。
③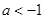 時,函數在
時,函數在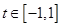 上單調遞減,有
上單調遞減,有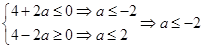
綜上所述: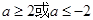 。
。
考點:本題主要考查正弦函數的值域,二次函數圖象和性質,簡單不等式組的解法。
點評:中檔題,通過換元,將問題轉化成二次函數在閉區間的最值問題。研究二次函數在閉區間的最值問題,要注意“二次項系數的正負,對稱軸的位置,區間端點的函數值”,一般有兩種情況:一是“軸動區間定”,二是“軸動區間定”。(2)是討論方程解的情況,注意結合圖象進行分析,布列不等式組。


 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中數學 來源: 題型:解答題
已知定義在R上的函數f(x)= 的周期為
的周期為 ,
,
且對一切x R,都有f(x)
R,都有f(x) ;
;
(1)求函數f(x)的表達式;
(2)若g(x)=f( ),求函數g(x)的單調增區間.
),求函數g(x)的單調增區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com