
如圖,在正三棱柱ABC-A1B1C1中,BB1=BC=2,M是BC中點,點N在CC1上.
(1)試確定點N的位置,使AB1⊥MN;
(2)當AB1⊥MN時,求二面角M-AB1-N的大小.
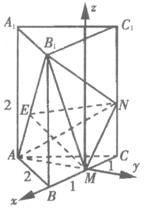
解法一:(1)連結MA,過M作MN⊥B1M交CC1于點N.
在正△ABC中,AM⊥BC,又平面ABC⊥平面BC1,
∴AM⊥平面BC1
又MN![]() 平面BC1 ∴MN⊥AM
平面BC1 ∴MN⊥AM
又XMN⊥B1M ∴MN⊥平面AMB1.
∴MN⊥AB1
在Rt△B1BM與Rt△MCN中,易知∠NMC=∠BB1M
∴tan∠NMC=![]() NC=tan∠B1BM=
NC=tan∠B1BM=![]()
即NC=![]()
(2)過點M作ME⊥AB1,垂足為E,連接EN由(1)知MN⊥平面AMB1
∴EN⊥AB1(三垂線定理)
∴∠MEN即為二面角M-AB1-N的平面角
由AM⊥平面BC1,知AM⊥B1M
在Rt△AMB1中,
AM=![]() ,B1M=
,B1M=![]() ,AB1=2
,AB1=2![]()
∴ME=![]() ,
,
又MN=![]()
故在Rt△EMN中,
tan∠MEN=![]()
故二面角M-ABl-N的大小為arctan![]()
解法二:(1)以點M為原點,建立如圖所示空間直角坐標系,

則:M(0,0,0),B(1,0,0),A(0,-![]() ,0),B1(1,0,2)令N(-1,0,z)
,0),B1(1,0,2)令N(-1,0,z)
∴![]() =(1,
=(1,![]() ,2),
,2),![]() =(-1,0,z)
=(-1,0,z)
由AB1⊥MN,知![]() ·
·![]() =-1+2z=0
=-1+2z=0
∴z=![]() ,即NC=
,即NC=![]()
(2)∵AM⊥BC,平面ABC⊥平面B1BCC1
∴AM⊥平面B1BCC1
∴AM⊥MN,又MN⊥AB1 ∴MN⊥平面AMB1
即![]() 為平面AB1M的法向量,
為平面AB1M的法向量,
且![]() =(-1,0,
=(-1,0,![]() )(8分)
)(8分)
設平面AB1N的法向量為n=(x,y,1),
且![]() =(1,
=(1,![]() ,2),
,2),![]() =(-1,
=(-1,![]() )
)
有 ∴
∴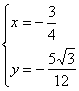
∴ n=(![]() ,1)
,1)
∴![]() ·n=
·n=![]()
而|![]() |=
|=![]() |n|=
|n|=![]() ∴cosθ=
∴cosθ=![]()
故二面角M-AB1-N的大小為arcos![]() .
.


科目:高中數學 來源: 題型:
 如圖,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小為60°,則點C到平面C1AB的距離為( )
如圖,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小為60°,則點C到平面C1AB的距離為( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在正三棱柱ABC-A1B1C1中,D、E、G分別是AB、BB1、AC1的中點,AB=BB1=2.
如圖,在正三棱柱ABC-A1B1C1中,D、E、G分別是AB、BB1、AC1的中點,AB=BB1=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中點,點N在AA1上,AN=
如圖,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中點,點N在AA1上,AN=| 1 | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•馬鞍山二模)如圖,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延長線上一點,過A、B、P三點的平面交FD于M,交EF于N.
(2012•馬鞍山二模)如圖,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延長線上一點,過A、B、P三點的平面交FD于M,交EF于N.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com